Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 715
Задание 715
\[\boxed{\mathbf{715.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[окружность\ (O;r);\]
\[AA_{1} - диаметр;\]
\[BB_{1} - хорда;\]
\[AA_{1}\bot BB_{1}.\]
\[\mathbf{Доказать:}\]
\[\cup AB = \cup AB_{1}.\]
\[\mathbf{Доказательство.}\]
\[1)\ BO = OB_{1} = r:\ \]
\[\mathrm{\Delta}BOB_{1} - равнобедренный.\]
\[2)\ AA_{1}\bot BB_{1} \Longrightarrow\]
\[\Longrightarrow \angle BDO = \angle ODB_{1} = 90{^\circ}.\]
\[3)\ \mathrm{\Delta}BDO = \mathrm{\Delta}ODB_{1}\ \]
\[(по\ гипотенузе\ и\ катету):\]
\[BO = OB_{1};\ \]
\[DO - общий\ катет.\]
\[Отсюда:\]
\[\angle BOD = \angle DOB_{1}.\]
\[4)\ \angle BOD = \cup AB\ и\ \]
\[\angle DOB_{1} = \cup AB_{1}\ \]
\[(как\ центральные\ углы);\]
\[\angle BOD = \angle DOB_{1}.\]
\[Значит:\ \]
\[\cup AB = \cup AB_{1}.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{715.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
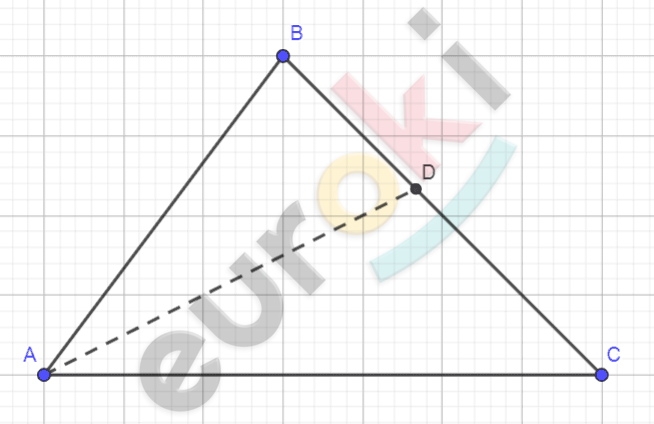
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
\[D \in BC;\]
\[\frac{\text{BD}}{\text{AB}} = \frac{\text{DC}}{\text{AC}}.\]
\[\mathbf{Доказать:}\]
\[AD - биссектриса\ \mathrm{\Delta}\text{ABC.}\]
\[\mathbf{Доказательство.}\]
\[\frac{\text{BD}}{\text{AB}} = \frac{\text{DC}}{\text{AC}} \Longrightarrow \frac{\text{BD}}{\text{DC}} = \frac{\text{AB}}{\text{AC}}\ \]
\[(задача\ 535).\]
\[Значит:\ \]
\[AD - биссектриса,\ так\ как\ \]
\[биссектриса\ \angle A\ делит\ BC\ \]
\[в\ соотношении\ \frac{\text{AB}}{\text{AC}}.\]
\[Что\ и\ требовалось\ доказать.\]
