Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 712
Задание 712
\[\boxed{\mathbf{712.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\mathbf{\ задачи:}\]
\[\mathbf{Дано:}\]
\[окружность\ (O;r);\]
\[AB - хорда;\]
\[AC,\ BC - касательные.\]
\[\mathbf{Доказать:}\]
\[AC \cap BC = C.\]
\[\mathbf{Доказательство.}\]
\[1)\ AO = OB = r:\]
\[\mathrm{\Delta}ABO - равнобедренный.\]
\[Отсюда:\ \]
\[\angle OAB = \angle OBA = \alpha.\]
\[2)\ По\ теореме\ о\ сумме\ углов\ в\ \]
\[треугольнике:\]
\[\angle AOB =\]
\[= 180{^\circ} - (\angle OAB + \angle OBA) =\]
\[= 180{^\circ} - 2\alpha.\]
\[3)\ \angle AOB =\]
\[= \cup AB\ (как\ центральный).\]
\[4)\ AC\bot AO\ \]
\[(так\ как\ AC - касательная):\]
\[\angle CAB = 90{^\circ} - \alpha.\]
\[5)\ \angle AOB = 180{^\circ} - 2\alpha\ и\ \]
\[\angle CAB = 90{^\circ} - \alpha:\]
\[\angle CAB = \frac{1}{2}\angle AOB = \frac{1}{2} \cup AB.\]
\[6)\ BC\bot OB\ \]
\[(так\ как\ BC - касательная):\]
\[\angle CBA = 90{^\circ} - \alpha\]
\[\angle CBA = \angle CAB = \frac{1}{2} \cup AB.\]
\[7)\ \cup AB < 180{^\circ}\ \]
\[\left( по\ условию\ \text{AB} - не\ диаметр \right):\]
\[о\ \angle CAB = \angle CBA < 90{^\circ}\]
\[\text{AC}\bot\text{AB\ }и\ \text{BC}\bot\text{AB.}\]
\[Следовательно:\ \]
\[AC \cap BC = C.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{712.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
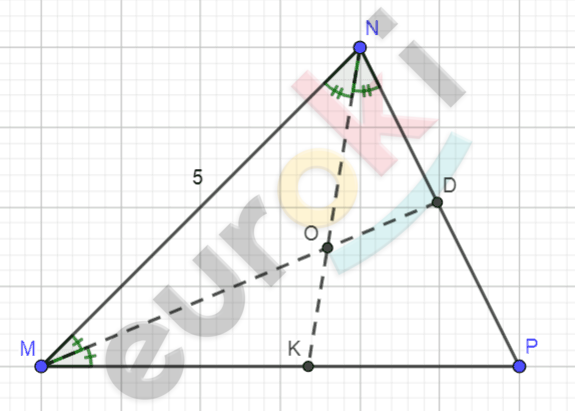
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}MNP;\]
\[\text{MD\ }и\ NK - биссектрисы;\]
\[MD \cap NK = O;\]
\[MN = 5\ см;\]
\[NP = 3\ см;\]
\[MP = 7\ см.\]
\[\mathbf{Найти:}\]
\[OK\ :ON - ?\]
\[\mathbf{Решение.}\]
\[1)\ Пусть\ MK = x;\ \]
\[KP = 7 - x\ см;\]
\[\frac{\text{MK}}{\text{KP}} = \frac{\text{MN}}{\text{NP}}\ (задача\ 535):\]
\[\frac{x}{7 - x} = \frac{5}{3}\]
\[\ 3x = (7 - x) \bullet 5\]
\[3x = - 5x + 35\]
\[8x = 35\]
\[x = \frac{35}{8} = 4\frac{3}{8}\ см.\]
\[4)\ MO - биссектриса\ \mathrm{\Delta}MKN:\]
\[\frac{\text{OK}}{\text{ON}} = \frac{\text{MK}}{\text{MN}}\]
\[\frac{\text{OK}}{\text{ON}} = \frac{35}{8}\ :5 = \frac{35}{8} \bullet \frac{1}{5} = \frac{7}{8}.\]
\[\mathbf{Ответ:}\frac{\text{OK}}{\text{MN}} = \frac{7}{8}.\]
