Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 703
Задание 703
\[\boxed{\mathbf{703.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC - равнобедренный,\]
\[вписанный\ в\ окружность;\]
\[AB - диаметр;\]
\[\cup BC = 102{^\circ}.\]
\[\mathbf{Найти:}\]
\[\textbf{а)}\ \angle ABC;\ \angle ACB;\]
\[\angle BAC - ?\]
\[\textbf{б)}\ \angle BCA^{'};\angle CBA^{'};\]
\[\angle BA^{'}C - ?\]
\[\mathbf{Решение.}\]
\[\textbf{а)}\ 1)\ \angle BAC = \frac{1}{2} \cup BC = \frac{102{^\circ}}{2} =\]
\[= 51{^\circ}\ (как\ вписанный\ \ угол);\]
\[2)\ \angle ABC = \angle ACB =\]
\[= \frac{180{^\circ} - 51{^\circ}}{2} = 64{^\circ}30^{'}\ \]
\[(\mathrm{\Delta}ABC - равнобедренный).\]
\[\textbf{б)}\ 1)\ \angle BA^{'}C = \frac{1}{2} \cup BC =\]
\[= \frac{(360{^\circ} - 102{^\circ})}{2} = \frac{258{^\circ}}{2} = 129{^\circ}\]
\[(как\ вписаный\ угол);\]
\[2)\ \angle BCA^{'} = \angle CBA^{'} =\]
\[= \frac{180{^\circ} - 129{^\circ}}{2} = 25{^\circ}30^{'}\ \]
\[(\mathrm{\Delta}ABC - равнобедренный).\]
\[Ответ:а)\ \angle BAC = 51{^\circ};\ \]
\[\angle ABC = \angle ACB = 64{^\circ}30';\]
\[\textbf{б)}\ \angle BA'C = 129{^\circ};\]
\[\angle BCA^{'} = \angle CBA^{'} = 25{^\circ}30'.\ \]
\[\boxed{\mathbf{703.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
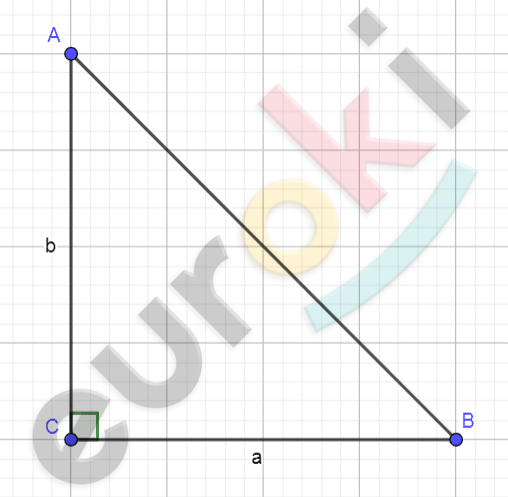
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC - прямоугольный;\]
\[\angle C = 90{^\circ};\]
\[AC = b;\ \]
\[CB = b;\]
\[a = 12;\]
\[b = 15.\]
\[\mathbf{а)\ Выразить:}\]
\[\text{AB\ },tg\ \angle A,\ tg\ \angle B\]
\[через\ a\ и\text{\ b.}\]
\[\textbf{б)}\ Найти:\]
\[AB;\ \ tg\ \angle A;\ \ \ tg\ \angle B.\]
\[\mathbf{Решение.}\]
\[\textbf{а)}\ AB = \sqrt{a^{2} + b^{2}}\ \]
\[(по\ теореме\ Пифагора);\]
\[\textbf{б)}\ AB = \sqrt{a^{2} + b^{2}} =\]
\[= \sqrt{144 + 225} = \sqrt{369} = 19,2.\]
\[tg\ \angle A = \frac{a}{b} = \frac{12}{15} \Longrightarrow \angle A = 38{^\circ}39^{'}.\]
\[tg\ \angle B = \frac{b}{a} = \frac{15}{12} \Longrightarrow \angle B = 51{^\circ}21^{'}.\]
\[\mathbf{Ответ:}\mathbf{а)}\ AB = \sqrt{a^{2} + b^{2}};\]
\[tg\ \angle A = \frac{a}{b};tg\ \angle B = \frac{b}{a};\]
\[\textbf{б)}\ AB = 19,2;\angle A = 38{^\circ}39^{'};\ \]
\[\angle B = 51{^\circ}21^{'}.\]
