Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 702
Задание 702
\[\boxed{\mathbf{702.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC - вписанный\ в\ \]
\[окружность;\]
\[AB - диаметр;\]
\[\textbf{а)} \cup BC = 134{^\circ};\]
\[\textbf{б)} \cup AC = 70{^\circ}.\]
\[\mathbf{Найти:}\]
\[\angle CAB - ?\ \]
\[\angle ACB - ?\]
\[\angle CBA - ?\]
\[\mathbf{Решение.}\]
\[\angle ACB = 90{^\circ} - так\ как\ угол\]
\[\ опирается\ на\ диаметр.\]
\[\textbf{а)}\ \angle CAB = \frac{1}{2} \cup BC = \frac{134{^\circ}}{2} =\]
\[= 67{^\circ}\ (как\ вписанный\ угол);\]
\[\textbf{б)}\ \angle CBA = \frac{1}{2} \cup AC = \frac{70{^\circ}}{2} =\]
\[= 35{^\circ}\ (как\ вписанный\ угол);\]
\[Ответ:а)\ \angle ACB = 90{^\circ};\ \]
\[\angle CAB = 67{^\circ};\ \angle CBA = 23{^\circ};\]
\[\textbf{б)}\ \angle ACB = 90{^\circ};\ \]
\[\angle CAB = 55{^\circ};\ \angle CBA = 35{^\circ}.\ \]
\[\boxed{\mathbf{702.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
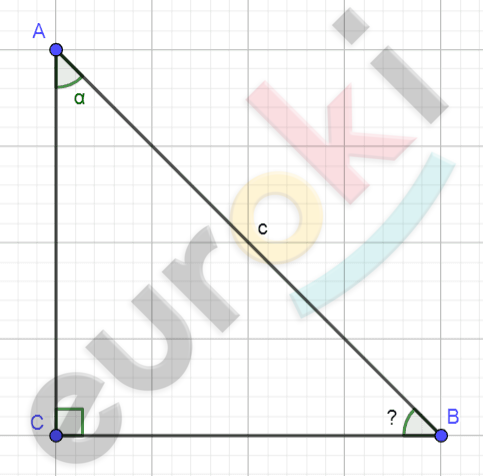
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC - прямоугольный;\]
\[\angle C = 90{^\circ};\]
\[AB = c;\ \]
\[\angle A = \alpha;\]
\[c = 24\ см;\]
\[\alpha = 35{^\circ}.\]
\[\mathbf{а)\ Выразить:}\]
\[BC;\ AC;\ \angle B\ через\]
\[\alpha\ и\ c;\]
\[\textbf{б)}\ Найти:\]
\[\angle B;BC\ и\ AC - ?\]
\[\mathbf{Решение.}\]
\[\textbf{а)}\ \cos\alpha = \frac{\text{AC}}{\text{AB}}\]
\[AC = c \bullet \cos\alpha.\ \]
\[\sin\alpha = \frac{\text{BC}}{\text{AB}}\]
\[BC = c \bullet \sin\alpha.\ \]
\[По\ свойству\ прямоугольного\ \]
\[треугольника:\]
\[\angle B = 90{^\circ} - \text{α.}\]
\[\textbf{б)}\ \angle B = 90{^\circ} - \alpha = 90{^\circ} - 35{^\circ} =\]
\[= 55{^\circ}.\]
\[BC = c \bullet \sin\alpha = 24 \bullet \sin{35{^\circ}} =\]
\[= 24 \bullet 0,5736 = 14\ см.\]
\[AC = c \bullet \cos\alpha = 24 \bullet \sin{35{^\circ}} =\]
\[= 24 \bullet 0,8192 = 20\ см.\]
\[\mathbf{Ответ:}\mathbf{а)}\ BC = c \bullet \sin\alpha;\ \]
\[AC = c \bullet \cos\alpha\ ;\ \angle B = 90{^\circ} - \alpha;\]
\[\textbf{б)}\ \angle B = 55{^\circ};BC = 14\ см;\]
\[AC = 20\ см.\]
