Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 693
Задание 693
\[\boxed{\mathbf{693}\mathbf{.}\mathbf{ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC - прямоугольный;\]
\[прямоугольн;\]
\[\angle C = 90{^\circ};\]
\[\textbf{а)}\ AB = 26\ см;\]
\[r = 4\ см;\]
\[\textbf{б)}\ AD = 5\ см;\]
\[DB = 12\ см.\]
\[\mathbf{Найти:}\]
\[P_{\text{ABC}} - ?\]
\[\mathbf{Решение.}\]
\[\textbf{а)}\ 1)\ FOEC - четырехугольник;\ \]
\[\angle OFC = \angle FOE = \angle OEC =\]
\[= \angle ECF = 90{^\circ};\]
\[\ FO = OE.\]
\[Значит:\ \]
\[FOEC - квадрат \Longrightarrow\]
\[\Longrightarrow FC = CE = OE = FO = 4\ см.\]
\[2)\ AF = AD;\ \ BD = BE\ \]
\[(по\ теореме\ о\ касательных).\]
\[3)\ AB = AD + DB.\]
\[4)\ P_{\text{ABC}} = AB + BC + AC =\]
\[= AB + CE + EB + AF + FC;\]
\[P_{\text{ABC}} =\]
\[= AB + CE + FC + BD + AD =\]
\[= 26 + 4 + 4 + 4 + AB =\]
\[= 26 + 4 + 4 + 26 = 60\ см.\]
\[\textbf{б)}\ 1)\ AB = AD + DB = 5 + 12 =\]
\[= 17\ см.\]
\[2)\ По\ теореме\ о\ касательных\ к\ \]
\[окружности:\]
\[AF = AD = 5\ см;\ \]
\[BD = BE = 12\ см.\]
\[3)\ AC = AF + r = 5 + r;\ \ \ \]
\[BC = BE + r = 12 + r.\]
\[4)\ По\ теореме\ Пифагора:\]
\[(5 + r)^{2} + (12 + r)^{2} = 17^{2}\]
\[25 + 10r + r^{2} + 144 + 24r + r^{2} =\]
\[= 289\]
\[2r^{2} + 34r - 120 = 0\]
\[r^{2} + 17r - 60 = 0\]
\[По\ теореме\ Виета:\]
\[r_{1} + r_{2} = - 17;\ \ \ r_{1} \bullet r_{2} = - 60\ \]
\[r_{1} = 3;\ \ r_{2} = - 20.\ \]
\[Значит:\ \]
\[r = 3\ см.\]
\[5)\ AC = 5 + 3 = 8\ см;\]
\[BC = 12 + 3 = 15\ см.\]
\[5)\ P_{\text{ABC}} = AB + BC + AC =\]
\[= 17 + 15 + 8 = 40\ см.\]
\[Ответ:а)\ 60\ см;\ \]
\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ б)\ 40\ см.\ \]
\[\boxed{\mathbf{693.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
\[\mathbf{Построить}\mathbf{:}\]
\[\mathbf{треугольник\ по\ двум\ заданным\ }\]
\[\mathbf{углам\ и}\mathbf{\ }\mathbf{высоте,\ проведенной\ }\]
\[\mathbf{из\ третьего\ угла}\mathbf{.}\]
\[\mathbf{Построение.}\]
\[1)\ Строим\ продолжение\ сторон\ \]
\[большего\ угла,\ накладываем\ \]
\[второй\ угол\ на\ сторону\ \]
\[первого.\ Также\ строим\ \]
\[продолжение\ второй\ стороны.\]
\[2)\ Отмечаем\ на\ углах\ \]
\[точки\ \text{A\ }и\ B,\ а\ в\ месте\ \]
\[пересечения - точку\ \text{C.}\]
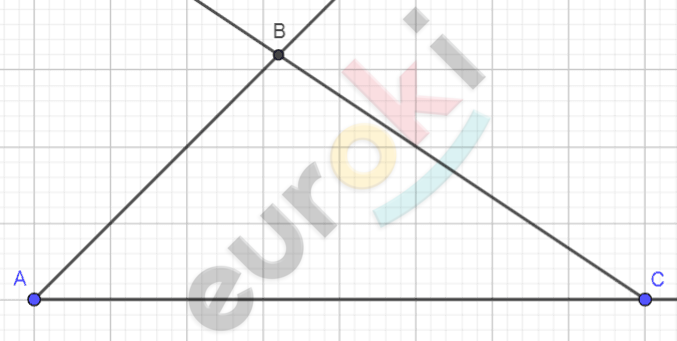
\[3)\ Через\ точку\ \text{B\ }проводим\ \]
\[перпендикуляр\ к\ прямой\ \text{AC.}\]
\[4)\ На\ прямой\ \text{AC\ }отмечаем\ \]
\[отрезок\ MH,\ равный\ высоте.\]
\[5)\ Через\ точку\ \text{M\ }проводим\ \]
\[прямые,\ параллельные\ \text{AB\ }и\ \]
\[\text{BC.}\]
\[6)\ На\ пересечении\ данных\ \]
\[прямых\ и\ \text{AC\ }отмечаем\ \]
\[точки\ \text{N\ }и\ \text{K.}\]
\[7)\ \mathrm{\Delta}MNK - искомый.\]
