Решебник по геометрии 7 класс Атанасян ФГОС Задание 692

 

\[\boxed{\mathbf{692.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[\mathrm{\Delta}ABC;\]

\[AB = 10\ см;\]

\[BC = 12\ см;\]

\[CA = 5\ см.\]

\[\mathbf{Найти:}\]

\[AD,\ AE,\ EB,\]

\[BF,\ FC,\ CD.\]

\[\mathbf{Решение.}\]

\[1)\ По\ свойству\ касательныъ\ к\ \]

\[окружности:\ \]

\[AD = AE;EB = BF;FC = CD.\]

\[2)\ Пусть\ EB = x;\ \ \ AE = 10 - x;\ \ \]

\[FC = 1 - x:\]

\[AC = AD + DC = AE + FC\]

\[5 = 10 - x + 12 - x;\]

\[2x = 17\]

\[x = 8,5.\]

\[EB = BF = 8,5\ см.\]

\[3)\ AE = AD = 10 - 8,5 = 1,5\ см.\]

\[4)\ CD = FC = 12 - 8,5 = 3,5\ см.\]

\[Ответ:CD = FC = 3,5\ см;\]

\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ AE = AE = 1,5\ см;\]

\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ EB = BF = 8,5\ см.\ \]

\[\boxed{\mathbf{692.еуроки - ответы\ на\ пятёрку}}\]

\[\mathbf{Дано:}\]

\[\mathbf{Построить}\mathbf{:}\]

\[\mathbf{треугольник\ по\ двум\ заданным\ }\]

\[\mathbf{углам\ и}\mathbf{\ }\mathbf{биссектрисе\ меньшего\ }\]

\[\mathbf{из\ них}\mathbf{.}\]

\[\mathbf{Построени}\mathbf{е.}\]

\[1)\ Строим\ продолжение\ сторон\ \]

\[большего\ угла,\ накладываем\ \]

\[второй\ угол\ на\ сторону\ первого.\ \]

\[Также\ строим\ продолжение\ \]

\[второй\ стороны.\]

\[2)\ Отмечаем\ на\ углах\ \]

\[точки\ \text{A\ }и\ B,\ а\ в\ месте\ \]

\[пересечения - \ точку\ \text{C.}\]

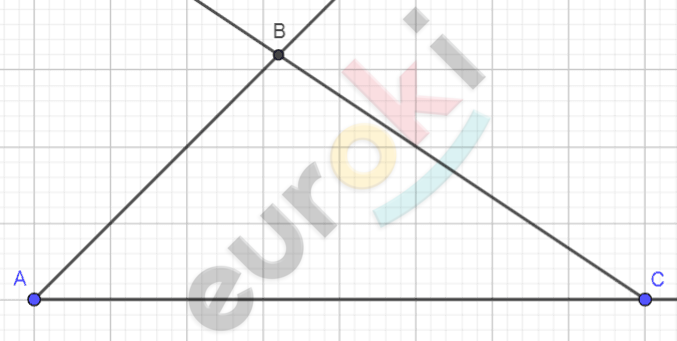
\[3)\ Внутри\ угла\ \text{C\ }отмечаем\ \]

\[точку,\ делящую\ угол\ пополам,\ \]

\[и\ проводим\ через\ нее\ луч\ СK.\]

\[4)\ На\ \text{CK\ }отмечаем\ \]

\[отрезок\ CC_{1} - равный\ \]

\[биссектрисе.\]

\[5)\ Проведем\ через\ C_{1}\ прямую,\]

\[параллельную\ AB,\ и\ отметим\ \]

\[на\ пересечении\ данной\ прямой\ \]

\[и\ сторон\ угла\ \text{C\ }точки\ \text{M\ }и\ N.\]

\[6)\ \mathrm{\Delta}MNC - искомый.\]