Решебник по геометрии 7 класс Атанасян ФГОС Задание 691

 

\[\boxed{\mathbf{691.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[\mathrm{\Delta}ABC - равнобедренный;\]

\[AB = BC;\]

\[BE = 4\ см;\]

\[AE = 3\ см.\]

\[\mathbf{Найти:}\]

\[P_{\text{ABC}} - ?\]

\[\mathbf{Решение.}\]

\[1)\ AB\ и\ AC - касательные\ к\ \]

\[окружности\ в\ точках\ E\ и\ K:\]

\[AE = AK = 3\ см\ \]

\[(по\ свойству\ касательных).\]

\[2)\ \mathrm{\Delta}ABC - равнобедренный:\]

\[AB = BC = AE + EB = 3 + 4 =\]

\[= 7\ см.\]

\[3)\ AK = KC = 3\ см\ \]

\[(так\ как\ BK - высота\ и\ медиана).\]

\[4)\ AC = AK + KC = 6\ см.\]

\[5)\ P_{\text{ABC}} = AB + AC + BC =\]

\[= 7 + 6 + 7 = 20\ см.\]

\[Ответ:P_{\text{ABC}} = 20\ см.\ \]

\[\boxed{\mathbf{691.еуроки - ответы\ на\ пятёрку}}\]

\[\mathbf{Дано}\mathbf{:}\]

\[Разделить\ отрезок\text{\ AB\ }\]

\[в\ отношении:\]

\[\textbf{а)}\ 2\ :5;\]

\[\textbf{б)}\ 3\ :7;\]

\[\textbf{в)}\ 4\ :3.\]

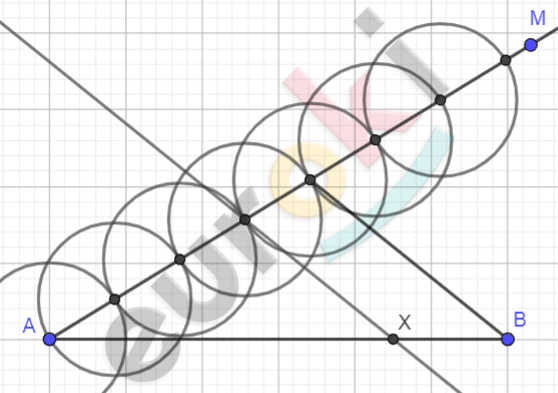
\[Построение.\]

\[Построим\ какй - нибудь\ \]

\[луч\ AM.\]

\[На\ данном\ луче\ при\ помощи\ \]

\[циркуля\ отложим\ 7\ равных\ \]

\[отрезков.\]

\[\textbf{а)}\ Проведем\ прямую\ от\ конца\ \]

\[5\ отрезка\ через\ точку\ B.\]

\[Построим\ прямую\ от\ конца\ \]

\[2\ отрезка,\ параллельную\ \]

\[данной\ прямой.\]

\[В\ точке\ пересечения\ \]

\[с\ отрезком\ \text{AB\ }отметим\ \]

\[точку\ \text{X.}\]

\[\textbf{б)}\ Проведем\ прямую\ от\ конца\ \]

\[7\ отрезка\ через\ точку\ \text{B.}\]

\[Построим\ прямую\ от\ конца\ \]

\[3\ отрезка,\ параллельную\ \]

\[данной\ прямой.\]

\[В\ точке\ пересечения\ \]

\[с\ отрезком\ \text{AB\ }отметим\ \]

\[точку\ \text{X.}\]

\[\textbf{в)}\ Проведем\ прямую\ от\ конца\ \]

\[4\ отрезка\ через\ точку\ \text{B.}\]

\[Построим\ прямую\ от\ конца\ \]

\[3\ отрезка,\ параллельную\ \]

\[данной\ прямой.\]

\[В\ точке\ пересечения\ \]

\[с\ отрезком\ \text{AB\ }отметим\ \]

\[точку\ \text{X.}\]