Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 657
Задание 657
\[\boxed{\mathbf{657.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[окружность\ (O,\ R);\ \]
\[\cup AB = 140{^\circ};\]
\(\cup AM\ :\ \cup BM = 6\ :5.\)
\[\mathbf{Найти:}\]
\[\angle BAM - ?\]
\[\mathbf{Решение.}\]
\[1)\ Пусть\ \cup AM = 6x;\ \]
\[\cup BM = 5x.\]
\[2)\ \cup AB = 360{^\circ} - 140{^\circ} = 220{^\circ}\]
\[\cup AM + \cup BM = 220{^\circ}\]
\[6x + 5x = 220{^\circ}\]
\[11x = 220{^\circ}\]
\[x = 20{^\circ}.\]
\[4)\ \cup BM = 5 \bullet 20{^\circ} = 100{^\circ}.\]
\[\angle BAM = \frac{1}{2} \cup BM = \frac{100{^\circ}}{2} = 50{^\circ}\ \]
\[(по\ теореме\ о\ вписанном\ угле).\]
\[Ответ:\angle BAM = 50{^\circ}.\]
\[\boxed{\mathbf{657.еуроки - ответы\ на\ пятёрку}}\]
\[\textbf{а)}\ Рисунок\ по\ условию\ задачи:\]
\[Дано:\ \]
\[\mathrm{\Delta}ABC;\ \mathrm{\Delta}CDE;\]
\[AB = 8;\]
\[AC = 12;\]
\[CD = 6;\]
\[ED = x;\ \]
\[\angle BCA = \angle E.\]
\[Найти:\]
\[ED - ?\]
\[Решение:\]
\[\frac{\text{AB}}{\text{DC}} = \frac{\text{BC}}{\text{CE}} = \frac{\text{AC}}{\text{DC}}\]
\[\frac{8}{6} = \frac{12}{x}\]
\[x = 9 \Longrightarrow ED = 9.\]
\[Ответ:ED = 9.\]
\[\textbf{б)}\ Рисунок\ по\ условию\ задачи:\]
\[Дано:\ \]
\[\mathrm{\Delta}ABC;\ \mathrm{\Delta}CDE;\]
\[AD = 20;\]
\[DC = 8;\]
\[EC = 10;\]
\[BA = y;\ \]
\[\angle A = \angle D = 90{^\circ}.\]
\[Найти:\]
\[BA - ?\]
\[Решение:\]
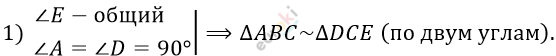
\[\frac{\text{AB}}{\text{DE}} = \frac{\text{AC}}{\text{DC}} = \frac{\text{BC}}{\text{EC}}.\]
\[2)\ DE = \sqrt{100 - 64} = 6;\]
\[\frac{\text{AB}}{6} = \frac{28}{8}\]
\[AB = 21.\]
\[Ответ:BA = 21.\]
