Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 658
Задание 658
\[\boxed{\mathbf{658.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[окружность\ (O,\ R);\ \]
\[AB - касател;\]
\[AD - секущая;\]
\[\cup BD = 110{^\circ}20^{'}.\]
\[\mathbf{Найти:}\]
\[\angle BAD - ?\ \]
\[\angle ADB - ?\]
\[\mathbf{Решение.}\]
\[1)\ \angle BKD - вписанный:\]
\[\angle BKD = \frac{1}{2} \cup BD\ \]
\[(по\ теореме\ о\ вписанном\ угле).\]
\[Отсюда:\]
\[\angle BKD = \frac{1}{2} \bullet 110{^\circ}20^{'} = 55{^\circ}10^{'}.\]
\[2)\ O \in AD\ и\ \]
\[K \in AD \Longrightarrow \cup KD = 180{^\circ}.\]
\[3)\ \angle DBK - вписанный:\ \]
\[\angle DBK = \frac{1}{2} \cup KD\ \]
\[(по\ теореме\ о\ вписанном\ угле).\]
\[Отсюда:\]
\[\angle DBK = \frac{1}{2} \bullet 180{^\circ} = 90{^\circ}.\]
\[4)\ В\ \ \ \mathrm{\Delta}DBK:\]
\[\angle D = 180{^\circ} - \angle BKD - \angle DBK =\]
\[= 90{^\circ} - 55{^\circ}10^{'} = 34{^\circ}50^{'}.\]
\[\angle ADB = \angle D = 34{^\circ}50^{'}.\]
\[5)\ \ \mathrm{\Delta}BOD - равнобедренный:\]
\[BO = OD = R.\]
\[Отсюда:\ \]
\[\angle DBO = \angle BDO = 34{^\circ}50^{'}.\]
\[6)\ \angle DBA = \angle DBO + \angle OBA =\]
\[= 34{^\circ}50^{'} + 90{^\circ} = 124{^\circ}50^{'}.\]
\[7)\ \angle BAD =\]
\[= 180{^\circ} - \left( 124{^\circ}50^{'} + 34{^\circ}50^{'} \right) =\]
\[= 20{^\circ}20^{'}.\]
\[Ответ:\angle BAD = 20{^\circ}20^{'};\ \]
\[\angle ADB = 34{^\circ}50'.\]
\[\boxed{\mathbf{658.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
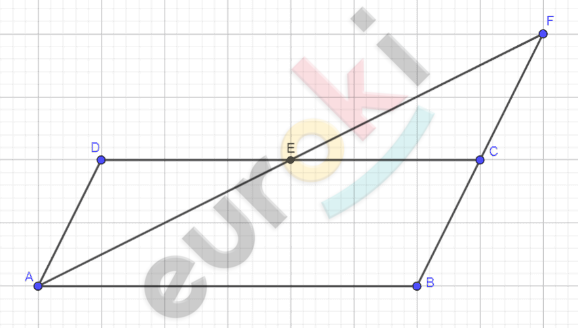
\[\mathbf{Дано:}\]
\[ABCD - параллелограмм;\]
\[AE \cap BC = F;\]
\[E \in DC;\]
\[\textbf{а)}\ DE = 8\ см;\]
\[EC = 4\ см;\]
\[BC = 7\ см;\]
\[AE = 10\ см;\]
\[\textbf{б)}\ AB = 8\ см;\]
\[AD = 5\ см;\]
\[CF = 2\ см.\]
\[\mathbf{Найти:}\]
\[\textbf{а)}\ EF;FC - ?\]
\[\textbf{б)}\ DE;EC - ?\]
\[\mathbf{Решение.}\]
\[\textbf{а)}\ \]
\[1)\ FB \parallel AD\ и\ AF - секущая:\]
\[\angle EAD = \angle EFC\ \]
\[(как\ накрестлежащие).\]
\[2)\ \mathrm{\Delta}ADE\sim\mathrm{\Delta}EFC\ \]
\[(по\ двум\ углам):\]
\[\angle DEA = \angle FEC\ \]
\[(как\ вертикальные);\ \]
\[\angle EAD = \angle EFC.\]
\[Отсюда:\]
\[\frac{\text{AE}}{\text{EF}} = \frac{\text{DE}}{\text{EC}} = \frac{\text{AD}}{\text{FC}} = k.\]
\[3)\frac{10}{\text{EF}} = \frac{8}{4} = \frac{7}{\text{FC}} = 2;\ \ \ k = 2.\]
\[4)\frac{10}{\text{EF}} = 2 \Longrightarrow EF = 5\ см;\]
\[\frac{7}{\text{FC}} = 2 \Longrightarrow FC = 3,5\ см.\]
\[\textbf{б)}\]
\[1)\ FB \parallel AD\ и\ AF - секущая:\]
\[\angle EAD = \angle EFC\ \]
\[(как\ накрестлежащие).\]
\[2)\ \mathrm{\Delta}ADE\sim\mathrm{\Delta}EFC\ \]
\[(по\ двум\ углам):\]
\[\angle DEA = \angle FEC\ \]
\[(как\ вертикальные);\ \]
\[\angle EAD = \angle EFC.\]
\[Отсюда:\]
\[\frac{\text{AE}}{\text{EF}} = \frac{\text{DE}}{\text{EC}} = \frac{\text{AD}}{\text{FC}} = k.\]
\[3)\frac{\text{AE}}{\text{EF}} = \frac{\text{DE}}{\text{EC}} = \frac{5}{2} = 2,5;\ \ \ k = 2,5.\]
\[4)AB = CD = 8 = DE + EC\]
\[EC = 8 - DE\]
\[\frac{\text{DE}}{8 - DE} = 2,5\]
\[DE = 20 - 2,5DE\]
\[3,5DE = 20\]
\[DE = 5\frac{5}{7}\ см.\]
\[5)\ EC = 8 - 5\frac{5}{7} = 2\frac{2}{7}\ см.\]
\[\mathbf{Ответ:}а)\ EF = 5\ см;\]
\[FC = 3,5\ см;\]
\[\textbf{б)}\ DE = 5\frac{5}{7}\ см;EC = 2\frac{2}{7}\ см\mathbf{.}\]
