Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 601
Задание 601
\[\boxed{\mathbf{601.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[ABCD - ромб;\]
\[AC = 2;\]
\[BD = 2\sqrt{3}.\]
\[\mathbf{Найти:}\]
\[\angle A - ?\]
\[\angle B - ?\]
\[\mathbf{Решение.}\]
\[1)\ ABCD - ромб.\ По\ свойству\ \]
\[диагоналей\ ромба:\]
\[AO = OC = 2\ :2 = 1;\]
\[BO = OD = 2\sqrt{3}\ :2 = \sqrt{3}.\]
\[2)\ \mathrm{\Delta}AOB - прямоугольный:\]
\[tg\ \angle BAO = \frac{\text{BO}}{\text{AO}} = \frac{\sqrt{3}}{1} = \sqrt{3};\]
\[\ \angle BAO = 60{^\circ}.\]
\[3)\ \angle ABO = 90{^\circ} - 60{^\circ} = 30{^\circ}.\]
\[4)\ По\ свойству\ диагоналей\ \]
\[ромба:\]
\[\text{AC\ }и\ BD - биссектрисы\ \]
\[\angle A\ и\ \angle B.\]
\[Отсюда:\ \]
\[\angle A = 2\angle BAO = 120{^\circ};\]
\[\angle B = 2\angle ABO = 60{^\circ}.\]
\[5)\ По\ определению\ ромба:\]
\[\angle A = \angle C = 120{^\circ};\ \]
\[\angle B = \angle D = 60{^\circ}.\ \]
\[\mathbf{Ответ:}\angle A = \angle C = 120{^\circ};\ \]
\[\angle B = \angle D = 60{^\circ}.\]
\[\boxed{\mathbf{601.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
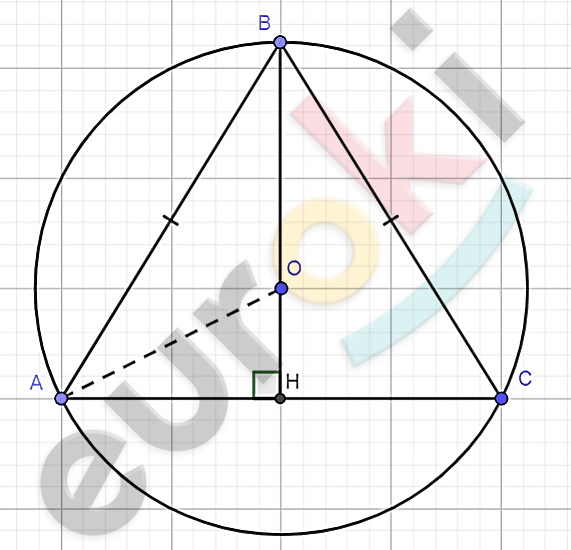
\[\mathrm{\Delta}ABC - равносторонний,\ \]
\[вписанный\ в\ окружность;\]
\[r = 10\ см.\]
\[\mathbf{Найти:}\]
\[AB - ?\]
\[\mathbf{Решение.}\]
\[1)\ \mathrm{\Delta}ABC - равносторонний:\]
\[AB = BC = AC\ \]
\[(по\ определению).\]
\[2)\ BH - высота\ и\ медиана\ и\ \]
\[AO - биссектриса\]
\[3)\ \mathrm{\Delta}AOH - прямоугольный:\]
\[\angle OAH = \frac{\angle A}{2} = \frac{60{^\circ}}{2} = 30{^\circ}\ \]
\[(так\ как\ AO - биссектр.);\]
\[AO = r = 10\ см;\]
\[\frac{\text{AH}}{\text{AO}} = cos\angle OAH \Longrightarrow\]
\[\Longrightarrow \ AH = 10 \bullet \cos{30{^\circ}} = 10\frac{\sqrt{3}}{2} =\]
\[= 5\sqrt{3}\ см.\]
\[4)\ AB = AH + HC = 2AH =\]
\[= 2 \bullet 5\sqrt{3} = 10\sqrt{3}\ см.\]
\[Ответ:AB = 10\sqrt{3}\ см.\]
