Решебник по геометрии 7 класс Атанасян ФГОС Задание 54

 

\[\boxed{\mathbf{54.}\mathbf{ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Начертим\ острый\ угол\ \text{AOB\ }и\ \]

\[отметим\ точку\ D\ на\ \]

\[продолжении\ луча\ OB:\]

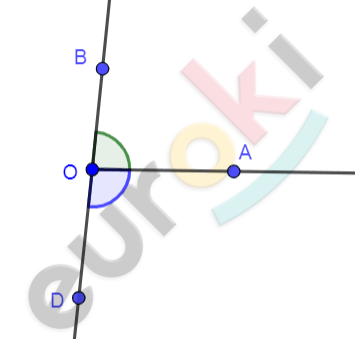
\[Углы\ \angle AOB\ и\ \angle AOD\ являются\ \]

\[смежными,\ а\ сумма\ смежных\ \]

\[углов\ равна\ 180{^\circ}.\]

\[Так\ как\ угол\ AOB < 90{^\circ},\ \]

\[то\ угол\ AOD > 90{^\circ},\ \]

\[следовательно:\ \]

\[\angle AOD > \angle AOB.\]

\[\boxed{\mathbf{54.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи.\]

\[Дано:\]

\[\angle AOC = 108{^\circ}\]

\[\angle\text{AOB} = \ 3\angle BOC\]

\[Найти:\]

\[\angle AOB - ?\]

\[Решение.\]

\[По\ условию\ задачи\ угол\ \text{AOB\ }\]

\[является\ частью\ угла\ AOC:\]

\[\angle AOC = \angle AOB + \angle BOC.\]

\[Пусть\ \angle BOC = x,\ \]

\[тогда\ \angle AOB = 3x.\]

\[Составим\ уравнение:\]

\[108{^\circ} = 3x + x\]

\[108{^\circ} = 4x\]

\[4x = 108{^\circ}\]

\[x = \frac{108}{4}\]

\[x = 27{^\circ}.\]

\[\angle AOB = 3 \bullet 27{^\circ} = 81{^\circ}.\]

\[Ответ:81{^\circ}.\]