Решебник по геометрии 7 класс Атанасян ФГОС Задание 528

 

\[\boxed{\mathbf{528.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[\text{ABCD} - трапеция;\]

\[\text{CD} = 12\ см;\]

\[\text{OF} = 5\ см;\]

\[\text{BD} \cap \text{AC} = O.\]

\[\mathbf{Найти:}\]

\[S_{\text{AOB}} - ?\]

\[\mathbf{Решение.}\]

\[1)\ S_{\text{COD}} = \frac{1}{2}\text{CD} \bullet \text{OF} =\]

\[= \frac{1}{2} \bullet 12 \bullet 5 = 30\ см^{2}.\]

\[2)\ Рассмотрим\ \mathrm{\Delta}\text{ABD}\ и\ \mathrm{\Delta}\text{ACD}:\]

\[S_{\text{ABD}} = \frac{1}{2}\text{AD} \bullet \text{BH};\]

\[S_{\text{ACD}} = \frac{1}{2}\text{AD} \bullet \text{CE};\ \]

\[\text{BH} = \text{CE}\ (как\ высоты).\]

\[Значит:\ \]

\[S_{\text{ABD}} = S_{\text{ACD}}.\]

\[3)\ S_{\text{ABD}} = S_{\text{ABO}} + S_{\text{AOD}};\]

\[S_{\text{ACD}} = S_{\text{COD}} + S_{\text{AOD}};\]

\[получаем:\]

\[S_{\text{AOB}} = S_{\text{COD}} = 30\ см^{2}.\]

\[\mathbf{Ответ:}30\ см^{2}.\]

\[\boxed{\mathbf{528.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи:\]

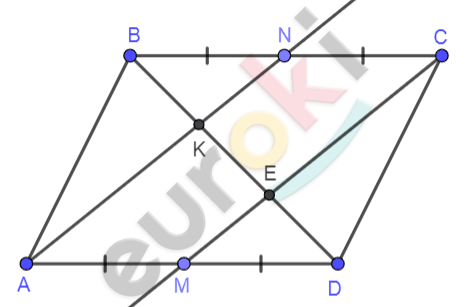
\[\mathbf{Дано:}\]

\[ABCD - параллелограмм;\]

\[AM = MD;\]

\[BN = NC;\]

\[AN \cap BD = K;\]

\[CM \cap BD = E.\]

\[\mathbf{Доказать:}\]

\[BK = KE = ED.\]

\[\mathbf{Доказательство.}\]

\[1)\ \mathrm{\Delta}ABN = \mathrm{\Delta}CDM - по\ двум\ \]

\[сторонам\ и\ углу\ между\ ними:\]

\[BN = MD\ \]

\[\left( так\ как\ \text{N\ }и\ M - середины \right);\]

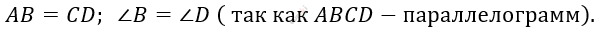
\[2)\ Соответствующие\ элементы\ \]

\[в\ равных\ фигурах\ равны:\]

\[AN = CM.\ \]

\[следовательно:\]

\[ANCM - параллелограмм;\]

\[\ AN \parallel CM.\]

\[4)\ BN = NC;\ \ AN \parallel CM:\]

\[BK = KE\ (по\ теореме\ Фалеса).\]

\[5)\ AM = MD;\ AN \parallel CM:\]

\[KE = ED\ (по\ теореме\ Фалеса).\]

\[6)\ BK = KE = ED.\]

\[\mathbf{Что\ и\ требовалось\ доказать.}\]