Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 436
Задание 436
\[\boxed{\mathbf{436.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\text{ABCD} - квадрат\]
\[\text{AC} - диагональ;\]
\[\text{AC} = 18,4\ см;\]
\[A \in l;\ l\bot\text{AC};\]
\[l \cap \text{BC} = M;\]
\[l \cap \text{CD} = N.\]
\[\mathbf{Найти:}\]
\[\text{MN} - ?\]
\[\mathbf{Решение.}\]
\[1)\ \text{ABCD} - квадрат:\ \]
\[\text{AC} - биссектрисса\ \angle С;\]
\[\ \angle\text{BCA} = \angle\text{ACD} = 45{^\circ}.\]
\[2)\ \angle\text{CAM} = 90{^\circ};\ \ \]
\[\angle\text{BCA} = 45{^\circ} \Longrightarrow \ \angle\text{CMA} = 45{^\circ}:\]
\[⊿\text{CAM} - равнобедренный;\ \]
\[\text{AM} = \text{AC} = 18,4\ см.\]
\[3)\ \angle\text{CAN} = 90{^\circ};\ \ \]
\[\angle\text{ACN} = 45{^\circ} \Longrightarrow \angle\text{CNA} = 45{^\circ}:\]
\[⊿\text{CAN} - равнобедренный;\]
\[\text{CA} = \text{AN} = 18,4\ см.\]
\[4)\ \text{MN} = \text{MA} + \text{AN} =\]
\[= 18,4 + 18,4 = 36,8\ см.\]
\[Ответ:36,8\ см.\]
\[\boxed{\mathbf{436.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
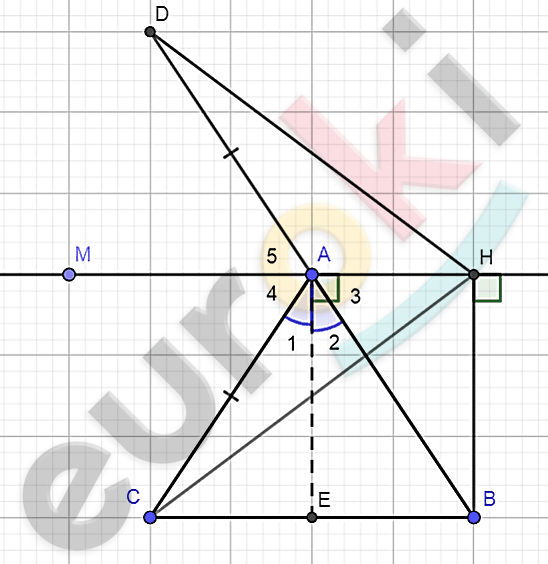
\[AE - биссектриса;\]
\[MH\bot AE;\]
\[BH\bot MH.\]
\[\mathbf{Доказать:}\]
\[P_{\text{BCH}} = P_{\text{ABC}}.\]
\[\mathbf{Доказательство.}\]
\[1)\ Продолжим\ отрезок\ \text{BA\ }\]
\[до\ отрезка\ AD = AC.\]
\[2)\ \angle 1 = \angle 2\ \]
\[(так\ как\ AE - биссектриса);\]
\[3)\ \angle 3 = 90{^\circ} - \angle 2\ \ и\ \angle 4 =\]
\[= 90{^\circ} - \angle 1\ (так\ как\ MH\bot AE):\]
\[\angle 1 = \angle 2 \Longrightarrow \angle 3 = \angle 4.\]
\[4)\ \angle 3 = \angle 5\ \]
\[(как\ вертикальные):\]
\[\angle 4 = \angle 5;\]
\[\angle DAH = 180{^\circ} - \angle 5;\ \]
\[\angle CAH = 180{^\circ} - \angle 4.\]
\[Получаем:\]
\[\angle DAH = \angle CAH.\]
\[5)\ \mathrm{\Delta}CAH = \mathrm{\Delta}DAH - по\ двум\ \]
\[сторонам\ и\ углу\ между\ ними:\]
\[AC = AD\ (по\ построению);\ \]
\[AH - общая\ сторона;\]
\[\angle DAH = \angle CAH.\ \]
\[Отсюда:\ \]
\[DH = CH.\]
\[6)\ DH + BH > DB\ \]
\[(по\ неравенству\ треугольника);\]
\[DB = DA + AB = CA + AB\ и\ \]
\[DH = CH:\]
\[CH + BH > AC + AB.\]
\[7)\ P_{\text{BCH}} = CH + BH + BC\ и\ \]
\[P_{\text{ABC}} = AB + BC + AC;\]
\[CH + BH > AC + AB.\]
\[Значит:\ P_{\text{BCH}} > P_{\text{ABC}}.\]
\[Что\ и\ требовалось\ доказать.\]
