Решебник по геометрии 7 класс Атанасян ФГОС Задание 435

 

\[\boxed{\mathbf{435.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[\mathrm{\Delta}\text{ABC};\]

\[D \in \text{AC};\]

\[K \in \text{BD};\]

\[\text{BK} = \text{KD}.\]

\[\mathbf{Доказать:}\]

\[\text{AM} = \text{MB};\]

\[\text{BN} = \text{NC}.\]

\[\mathbf{Доказательство.}\]

\[1)\ Пусть\ точка\ K -\]

\[середина\ \text{BD}\text{.\ }\]

\[Проведем\ через\ точку\ K\ \]

\[прямую,\ параллельную\ \text{AC}:\]

\[h \cap \text{AB} = M\ и\ h \cap \text{BC} = N.\]

\[Следовательно:\ \ \ \text{NM} \parallel \text{AC}.\]

\[2)\ \text{BK} = \text{KD};\ \ \ \text{MN} \parallel \text{AC}:\ \]

\[\text{MB} = \text{MA}\ (по\ теореме\ Фалеса).\]

\[Значит:\]

\[M - середина\ \text{AB}.\]

\[3)\ \text{BK} = \text{KD};\ \ \text{MN} \parallel \text{AC}:\ \]

\[\text{BN} = \text{NC}\ (по\ теореме\ Фалеса)\text{.\ }\]

\[Значит:\]

\[N - середина\ \text{BC}.\]

\[\mathbf{Что\ и\ требовалось\ доказать.}\]

\[\boxed{\mathbf{435.еуроки - ответы\ на\ пятёрку}}\]

\[\mathbf{Дано:}\]

\[\mathrm{\Delta}ABC;\]

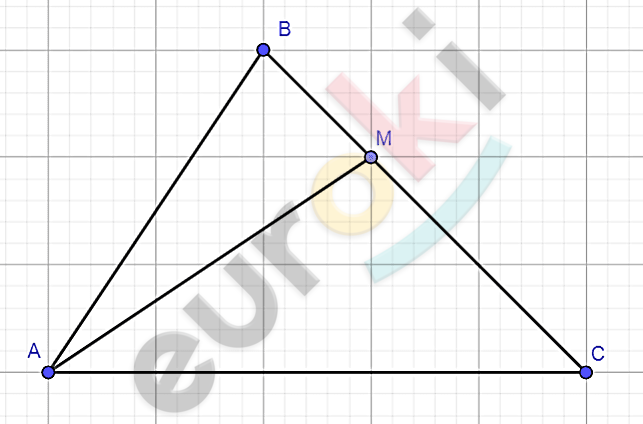
\[\text{AB} \neq AC;\]

\[M \in BC.\]

\[\mathbf{Доказать:}\]

\[\mathrm{\Delta}AMB \neq \mathrm{\Delta}AMC.\]

\[\mathbf{Доказательство.}\]

\[Предположим,\ что\ \]

\[\mathrm{\Delta}AMB = \mathrm{\Delta}AMC:\]

\[AM - общая\ сторона;\]

\[но\ это\ противоречит\ условию\ \]

\[задачи.\]

\[Значит:\]

\[\mathrm{\Delta}AMB \neq \mathrm{\Delta}AMC.\]

\[Что\ и\ требовалось\ доказать.\]