Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 428
Задание 428
\[\boxed{\mathbf{428.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\text{ABCD} - параллелограмм;\]
\[\text{AB} \neq \text{AD};\]
\[BB_{1};AA_{1};CC_{1};DD_{1} -\]
\[биссектрисы.\]
\[\mathbf{Доказать:}\]
\[\text{NMPS} - прямоугольник.\]
\[\mathbf{Доказательство.}\]
\[1)\ \text{ABCD} - параллелограмм:\]
\[\angle A = \angle C;\ \]
\[\angle B = \angle D.\]
\[2)\ \text{BC} \parallel \text{AD}\ и\ секущие\ \text{BA}\ и\ \text{CD}:\]
\[\angle A + \angle B =\]
\[= 180{^\circ}\ (как\ односторонние);\ \]
\[\angle C + \angle D =\]
\[= 180{^\circ}\ (как\ односторонние).\]
\[3)\ \angle\text{ABN} + \angle\text{BAN} =\]
\[= \frac{1}{2}\angle B + \frac{1}{2}\angle A = \frac{1}{2}(\angle B + \angle A) =\]
\[= \frac{1}{2} \bullet 180{^\circ} = 90{^\circ}.\]
\[4)\ \angle\text{PDC} + \angle\text{DCP} =\]
\[= \frac{1}{2}\angle D + \frac{1}{2}\angle C = \frac{1}{2}(\angle D + \angle C) =\]
\[= \frac{1}{2} \bullet 180{^\circ} = 90{^\circ}.\]
\[5)\ По\ сумме\ углов\ \]
\[треугольника:\]
\[\angle\text{ABN} + \angle\text{BAN} + \angle\text{BNA} = 180{^\circ};\ \]
\[\angle\text{BNA} = 90{^\circ};значит,\]
\[⊿\text{BNA} - прямоугольный.\]
\[По\ сумме\ углов\ треугольника:\]
\[\angle\text{PDC} + \angle\text{DCP} + \angle\text{CPD} = 180{^\circ};\ \]
\[\angle\text{CPD} = 90{^\circ};значит,\]
\[⊿\text{CPD} - прямоугольный.\]
\[6)\ \angle\text{MNS} = \angle\text{BNA} = 90{^\circ};\ \]
\[\angle\text{MPS} = \angle\text{CPD} =\]
\[= 90{^\circ}\ (как\ вертикальные\ углы).\]
\[7)\ \angle\text{CB}B_{1} =\]
\[= \angle BB_{1}A\ (как\ накрестлежащие);\]
\[\angle BB_{1}A =\]
\[= \angle\text{DDA}\ (как\ соответственные);\]
\[значит:\]
\[DD_{1} \parallel BB_{1}.\]
\[8)\ \angle\text{BA}A_{1} =\]
\[= \angle\text{DA}A_{1}(как\ накрестлежащие);\]
\[\angle AA_{1}B =\]
\[= \angle\text{BC}C_{1}\ (как\ соответственные);\ \]
\[значит:\]
\[AA_{1} \parallel CC_{1}.\]
\[9)\ \text{NMPS} - параллелограмм\ \]
\[(по\ определению);\]
\[\angle N = \angle P = 90{^\circ};\ \]
\[следовательно:\ \]
\[\text{NMPS} - прямоугольник.\]
\[\mathbf{Что\ и\ требовалось\ доказать.}\]
\[\boxed{\mathbf{428.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC - равнобедренный;\]
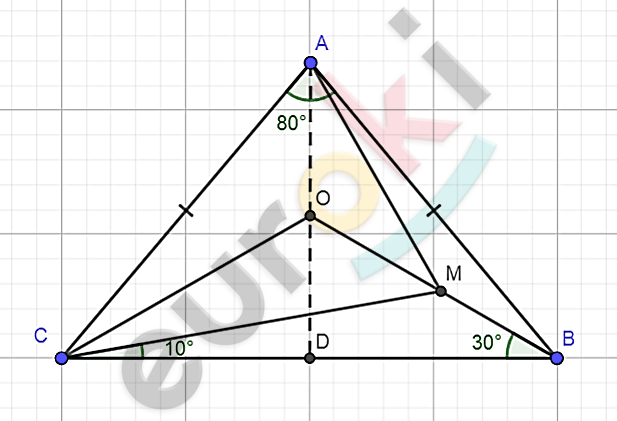
\[\angle MBC = 30{^\circ};\]
\[\angle MCB = 10{^\circ};\]
\[\angle BAC = 80{^\circ}.\]
\[\mathbf{Найти:}\]
\[\angle AMC - ?\]
\[\mathbf{Решение.}\]
\[1)\ \mathrm{\Delta}ABC - равнобедренный:\]
\[\angle C = \angle B = \frac{180{^\circ} - 80{^\circ}}{2} = 50{^\circ}.\]
\[2)\ Построим\ AD - высота,\ \]
\[медиана\ и\ биссектриса.\]
\[3)\ \mathrm{\Delta}AOC = \mathrm{\Delta}AOB - по\ двум\ \]
\[сторонам\ и\ углу\ между\ ними:\]
\[AO - общая;\ \]
\[\angle CAO = \angle OAB = 40{^\circ};\]
\[AC = AB.\]
\[Отсюда:\ \]
\[\angle AOC = \angle AOB\ и\ \angle ACO = \angle ABO.\]
\[4)\ \angle ACO = \angle ABO =\]
\[= 50{^\circ} - 30{^\circ} = 20{^\circ}.\]
\[5)\ \angle OCM = 50{^\circ} - 20{^\circ} - 10{^\circ} =\]
\[= 20{^\circ}.\]
\[6)\ \angle AOC = \angle AOB =\]
\[= 180{^\circ} - 20{^\circ} - 40{^\circ} = 120{^\circ}.\]
\[7)\ \angle COB = 360{^\circ} - 240{^\circ} = 120{^\circ}.\]
\[8)\ \mathrm{\Delta}ACO = \mathrm{\Delta}COM - по\ :\]
\[CO - общая;\ \]
\[\angle COA = \angle COM;\ \]
\[\angle ACO = \angle OCM.\]
\[Отсюда:\ \]
\[AC = CM.\]
\[9)\ В\ треугольнике\ AMC:\]
\[\angle AMC =\]
\[= 180{^\circ} - \angle ACM - \angle CAM =\]
\[= 180{^\circ} - 40{^\circ} - \angle CAM =\]
\[= 140{^\circ} - \angle CAM.\]
\[AC = CM \Longrightarrow \mathrm{\Delta}ACM -\]
\[равнобедренный.\]
\[Получаем:\]
\[\angle CAM = \angle CMA = \frac{180{^\circ} - 50{^\circ}}{2} =\]
\[= \frac{140{^\circ}}{2} = 70{^\circ}.\]
\[\angle AMC = 140{^\circ} - 70{^\circ} = 70{^\circ}.\]
\[Ответ:\ \angle AMC = 70{^\circ}.\]
