Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 425
Задание 425
\[\boxed{\mathbf{425.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\text{ABCD} - параллелограмм;\]
\[P_{\text{ABCD}} = 46\ см;\]
\[\text{AB} = 14\ см;\]
\[\text{AE} - биссектриса\ \angle A.\]
\[\mathbf{Найти:}\]
\[\textbf{а)}\ Какую\ сторону\ пересекает\ \]
\[\text{AE}?\]
\[\textbf{б)}\ Отрезки\ пересечения.\]
\[\mathbf{Решение.}\]
\[\textbf{а)}\ 1)\ P_{\text{ABCD}} =\]
\[= \text{AB} + \text{BC} + \text{CD} + \text{AD} =\]
\[= 2(\text{AB} + \text{AD})\]
\[46 = 2\left( 14 + \text{AD} \right)\]
\[23 = 14 + \text{AD}\]
\[\text{AD} = 9\ см.\]
\[\text{AD} < \text{AB} \Longrightarrow E \in \text{DC}.\]
\[\textbf{б)}\ 1)\ \text{CD} \parallel \text{AB}\ и\ \text{AE} - секущая:\]
\[\angle 3 =\]
\[= \angle 2\ (как\ накрестлежащие);\]
\[\angle 1 = \angle 2\ (по\ условию);\ \]
\[\angle 3 = \angle 1.\]
\[Значит:\]
\[\mathrm{\Delta}\text{ADE} - равнобедренный;\]
\[\text{AD} = \text{DE} = 9\ см.\]
\[2)\ \text{DC} = \text{DE} + \text{EC};\]
\[\text{EC} = 14 - 9 = 5\ см.\]
\[Ответ:а)\ \text{CD};\ \ б)\ \text{ED} = 9\ см;\]
\[\text{EC} = 5\ см.\]
\[\boxed{\mathbf{425.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
\[AM_{1},BM_{2},CM_{3} - биссектрисы;\]
\[QR\bot AM_{1};\]
\[QP\bot BM_{2};\]
\[RP\bot CM_{3}.\]
\[\mathbf{Доказать:}\]
\[\mathrm{\Delta}AQB\sim\mathrm{\Delta}BPC\sim\mathrm{\Delta}ARC.\]
\[\mathbf{Доказательство.}\]
\[1)\ \angle M_{1}AC = \angle BAM_{1} = \frac{1}{2}\angle BAC\ \]
\[\left( так\ как\ AM_{1} - биссектриса \right):\]
\[\angle CAR = \angle BAQ = 90{^\circ} - \frac{1}{2}\angle BAC.\]
\[2)\ \angle BCM_{3} = \angle ACM_{3} = \frac{1}{2}\angle BCA\ \]
\[\left( так\ как\ CM_{3} - биссектриса \right):\]
\[\angle BCP = \angle ACR = 90{^\circ} - \frac{1}{2}\angle BCA.\]
\[3)\ \angle ABM_{2} = \angle M_{2}BC = \frac{1}{2}\angle ABC\ \]
\[\left( так\ как\ BM_{2} - биссектриса \right):\]
\[\angle QBA = \angle CBP = 90{^\circ} - \frac{1}{2}\angle ABC.\]
\[4)\ \angle BPC =\]
\[= 180{^\circ} - \angle PBC - \angle PCB =\]
\[= \frac{1}{2}(180{^\circ} - \angle BAC) =\]
\[= 90{^\circ} - \frac{1}{2}\angle BAC.\]
\[5)\ \angle CRA =\]
\[= 180{^\circ} - \angle CAR - \angle ACR =\]
\[= 180{^\circ} - 90{^\circ} +\]
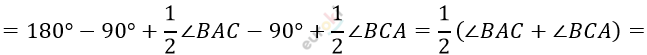
\[= \frac{1}{2}(180{^\circ} - \angle ABC) =\]
\[= 90{^\circ} - \frac{1}{2}\angle ABC.\]
\[6)\ \angle AQB =\]
\[= 180{^\circ} - \angle QAB - \angle QBA =\]
\[= \frac{1}{2}(180{^\circ} - \angle ACB) =\]
\[= 90{^\circ} - \frac{1}{2}\angle ACB.\]
\[7)\ Все\ углы\ треугольников\]
\[\mathrm{\Delta}AQB,\ \mathrm{\Delta}BPC\ и\ \mathrm{\Delta}ARC -\]
\[соответственно\ равны.\]
\[Что\ и\ требовалось\ доказать.\]
