Решебник по геометрии 7 класс Атанасян ФГОС Задание 420

 

\[\boxed{\mathbf{420.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[\mathrm{\Delta}\text{ABC} - равнобедренный;\]

\[\text{BH} - биссектрисса\ \angle B.\]

\[\mathbf{Доказать:}\]

\[\text{BH} - ось\ симметрии.\]

\[\mathbf{Доказательство.}\]

\[Прямая,\ содержащая\ \]

\[биссектриссу\ \text{BH},\ делит\ \mathrm{\Delta}\text{ABC}\ \]

\[на\ два\ равных\ прямоугольных\ \]

\[треугольника.\]

\[\text{BC} = \text{AB}\ (\text{BH} - медиана);\ \]

\[\text{AH} = \text{HC}\ \left( \text{BH} - медиана \right).\ \]

\[По\ признаку\ равенства\ \]

\[прямоугольных\ \]

\[треугольников\ \text{BH} - высота:\]

\[\ \text{BH} - ось\ симметрии.\]

\[\mathbf{Что\ и\ требовалось\ доказать.}\]

\[\boxed{\mathbf{420.еуроки - ответы\ на\ пятёрку}}\]

\[Дано:\ \]

\[\mathrm{\Delta}ABC\ и\ \mathrm{\Delta}A_{1}B_{1}C_{1};\ \]

\[\angle A = \angle A_{1};\ \]

\[AB = A_{1}B_{1};\]

\[AC + BC = A_{1}C_{1} + B_{1}C_{1}.\]

\[Доказать:\ \]

\[\mathrm{\Delta}ABC = \mathrm{\Delta}A_{1}B_{1}C_{1}.\]

\[Доказательство.\]

\[1)\ Построим\ \mathrm{\Delta}ABC\ по\ стороне,\ \]

\[углу\ и\ сумме\ двух\ других\ \]

\[сторон.\]

\[2)\ Возьмем\ угол\ A\ и\ на\ одной\ \]

\[его\ стороне\ отложим\ \]

\[отрезок\ AB,а\ на\ другой\ \]

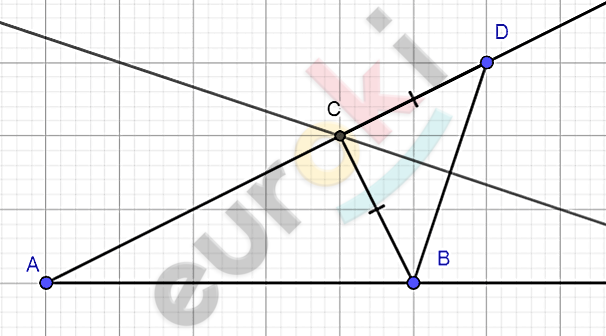
\[отрезок\ AD = AC + CB.\]

\[3)\ Построим\ серединный\ \]

\[перпендикуляр\ \text{DB\ }и\ отметим\ \]

\[точку\ C\ на\ пересечении\ с\ AD.\]

\[4)\ AC + CB = AD\ и\ AC + CD =\]

\[= AD \Longrightarrow CD = CB.\]

\[5)\ Таким\ образом,\ существует\ \]

\[лишь\ один\ вариант\ \]

\[построения\]

\[треугольника\ по\ углу,\ \]

\[прилежащей\ стороне\ и\ сумме\ \]

\[двух\ других\ сторон.\]

\[Следовательно:\ \]

\[\mathrm{\Delta}ABC = \mathrm{\Delta}A_{1}B_{1}C_{1}.\]

\[Что\ и\ требовалось\ доказать.\]