Решебник по геометрии 7 класс Атанасян ФГОС Задание 403

 

\[\boxed{\mathbf{403.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[ABCD - прямоугольник;\]

\[BD \cap AC = O;\]

\[\angle CAD = 30{^\circ};\]

\[AC = 12\ см.\]

\[\mathbf{Найти:}\]

\[P_{\text{AOB}} - ?\]

\[\mathbf{Решение.}\]

\[1)\ По\ свойству\ прямоугольного\ \]

\[треугольника:\]

\[CD = \frac{1}{2}AC = \frac{1}{2} \bullet 12 = 6\ см.\]

\[2)\ Диагонали\ делятся\ \]

\[точкой\ \text{O\ }пополам:\]

\[BO = OD = OC = AO = 6\ см.\]

\[3)\ P_{\text{AOB}} = AO + OB + AB =\]

\[= 6 + 6 + 6 = 18\ см.\]

\[Ответ:18\ см.\]

\[\boxed{\mathbf{403.еуроки - ответы\ на\ пятёрку}}\]

\[Дано:\]

\[a - ось\ симметрии;\]

\[b \parallel c.\]

\[Доказать:\]

\[b^{'} \parallel c^{'}.\]

\[Доказательство.\]

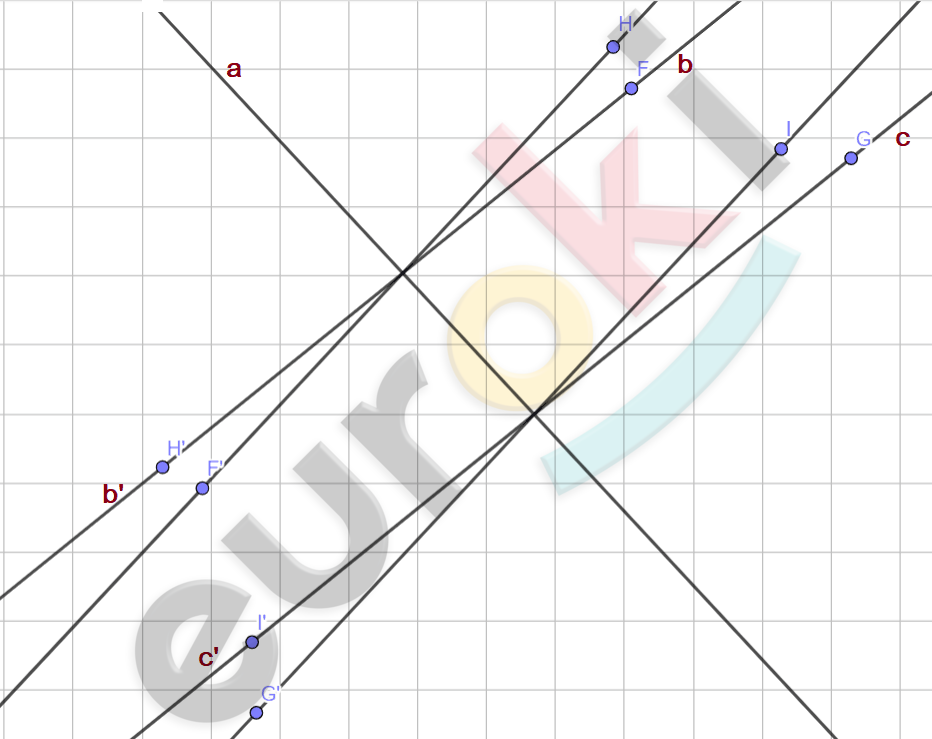
\[Отметим\ на\ прямой\ \text{b\ }\]

\[симметричные\ точки\ \text{F\ }и\ F^{'};\]

\[на\ прямой\ c\ симметричные\ \]

\[точки\ \text{G\ }и\ G^{'}.\]

\[Отметим\ на\ симметричных\ \]

\[прямых\ b^{'}и\ c^{'}\ симметричные\ \]

\[точки\ H\ и\ H^{'};I\ и\ I^{'}\ \]

\[соответственно.\]

\[Отрезок\ HH^{'},\ принадлежащий\ \]

\[прямой\ b^{'},\ перпендикулярен\ \]

\[прямой\ a:\]

\[b^{'}\bot a.\]

\[Отрезок\ II^{'},\ принадлежащий\ \]

\[прямой\ c^{'},\ перпендикулярен\ \]

\[прямой\ a:\]

\[c^{'}\bot a.\]

\[Две\ прямые,\ \]

\[перпендикулярные\ одной\ \]

\[прямой,\ параллельны:\]

\[b^{'} \parallel c^{'}.\]

\[Что\ и\ требовалось\ доказать.\]