Решебник по геометрии 7 класс Атанасян ФГОС Задание 379

 

\[\boxed{\mathbf{379.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[ABCD - параллелограмм;\]

\[AB \neq BC;\]

\[\angle A < 90{^\circ};\]

\[DM\bot AC;\]

\[BK\bot AC.\]

\[\mathbf{Доказать:}\]

\[BMDK - параллелограмм.\]

\[\mathbf{Доказательство.}\]

\[1)\ ABCD - параллелограмм:\]

\[BC \parallel AD\ и\ AC - секущая;\]

\[\angle BAC =\]

\[= \angle ACD\ (как\ накрест\ лежащие).\]

\[3)\ ⊿AKB = ⊿CMD - по\ второму\ \]

\[признаку\ равенства\ \]

\[прямоугольных\ треугольников.\]

\[5)\ DM\bot AC\ и\ BK\bot AC:\]

\[DM \parallel BK.\]

\[6)\ BMDK - прараллелограмм\ \]

\[(по\ признаку\ параллелограмма).\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{379.еуроки - ответы\ на\ пятёрку}}\]

\[\textbf{а)}\ отрезок\ \text{AB.}\]

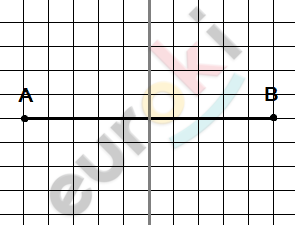
\[\textbf{б)}\ угол\ hk.\]

\[\mathbf{в)\ равнобедренный\ }\]

\[\mathbf{треугольник.}\]

\[\mathbf{г)\ разносторонний\ }\]

\[\mathbf{треугольник:}\]

\[\mathbf{нет\ оси\ симметрии.}\]

\[\mathbf{д)\ равносторонний\ }\]

\[\mathbf{треугольник.}\]