Решебник по геометрии 7 класс Атанасян ФГОС Задание 365

 

\[\boxed{\mathbf{365.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Формула\ суммы\ углов\ \]

\[выпуглого\ многоугольника:\]

\[(n - 2) \bullet 180{^\circ};\ \ \ \]

\[где\ n - количество\ углов.\]

\[Формула\ нахождения\ \]

\[количества\ углов:\]

\[dn = (n - 2) \bullet 180{^\circ};\ \]

\[где\ d - величина\ одного\ угла.\]

\[360{^\circ} = 180{^\circ}n - dn\]

\[n = \frac{360{^\circ}}{180{^\circ} - d}.\]

\[\textbf{а)}\ d = 90{^\circ}:\]

\[n = \frac{360{^\circ}}{180{^\circ} - 90{^\circ}} = 4.\]

\[\textbf{б)}\ d = 60{^\circ}:\]

\[n = \frac{360{^\circ}}{180{^\circ} - 60{^\circ}} = 3.\]

\[\textbf{в)}\ d = 120{^\circ}:\]

\[n = \frac{360{^\circ}}{180{^\circ} - 120{^\circ}} = 6.\]

\[\textbf{г)}\ d = 108{^\circ}:\]

\[n = \frac{360{^\circ}}{180{^\circ} - 108{^\circ}} = 5.\ \]

\[\boxed{\mathbf{365.еуроки - ответы\ на\ пятёрку}}\]

\[\mathbf{Дано:}\]

\[\mathbf{треугольники}\]

\[\mathbf{а)\ остроугольный}\mathbf{;}\]

\[\mathbf{б)\ прямоугольный}\mathbf{;}\]

\[\mathbf{в)\ тупоугольный}\mathbf{.}\]

\[\mathbf{Построить:}\]

\[\mathbf{вписанную\ окружность}\mathbf{.}\]

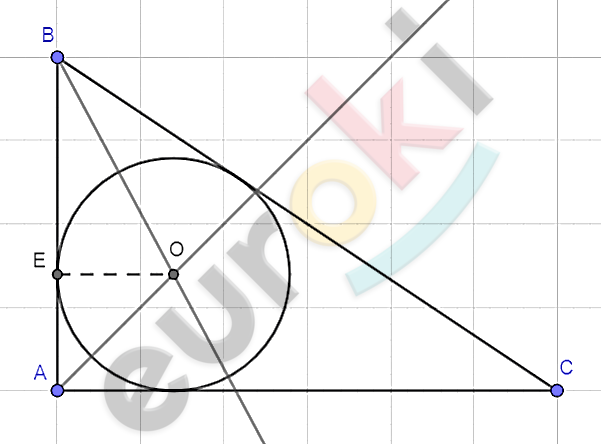
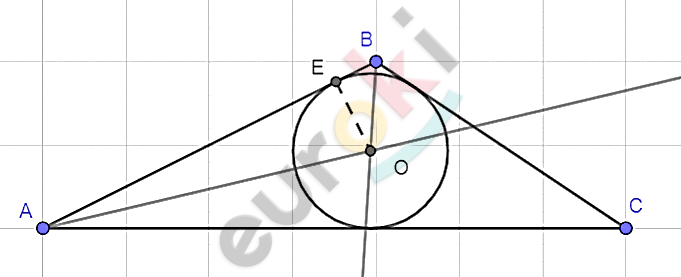
\[\mathbf{Построение.}\]

\[1)\ Строим\ биссектриссы\ \]

\[двух\ углов\ и\ на\ пересечении\ \]

\[отмечаем\ точку\ O.\]

\[2)\ Из\ точки\ \text{O\ }восстанавливаем\ \]

\[перпендикуляр\ к\ одной\ из\ \]

\[сторон\ треугольника,\ отмечаем\ \]

\[на\ пересечении\ \]

\[перпендикуляра\ и\ стороны\]

\[точку\ \text{E.}\]

\[3)\ Строим\ окружность\ (O;OE).\]

\[\textbf{а)}\]

\(\ \)

\[\textbf{б)}\]

\(\ \)

\[\textbf{в)}\]

\(\ \)

\[\mathbf{Центром\ вписанной\ }\]

\[\mathbf{в\ треугольник\ окружности\ }\]

\[\mathbf{является\ точка}\mathbf{\ }\mathbf{пересечения\ }\]

\[\mathbf{биссектрис\ углов\ }\]

\[\mathbf{треугольника}\mathbf{.}\]