Решебник по геометрии 7 класс Атанасян ФГОС Задание 321

 

\[\boxed{\mathbf{321.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Дано:\]

\[\angle A = 90{^\circ}.\]

\[Построить:\]

\[на\ стороне\ \text{AB\ }точку\ \text{M\ }\]

\[равноудаленную\ от\ \text{A\ }и\ \text{BC.}\]

\[Построение.\]

\[1)\ Отложим\ отрезок\ \text{CH\ }на\ \]

\[стороне\ \text{BC\ }равный\ стороне\ \text{AC.}\]

\[2)\ Построим\ серединный\ \]

\[перпендикуляр\ к\ отрезку\ \text{AH.}\]

\[3)\ На\ пересечении\ \]

\[серединного\ перпендикуляра\ \]

\[и\ стороны\ AB\ отметим\ \]

\[точку\ M - искомую.\]

\[\boxed{\mathbf{321.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи:\]

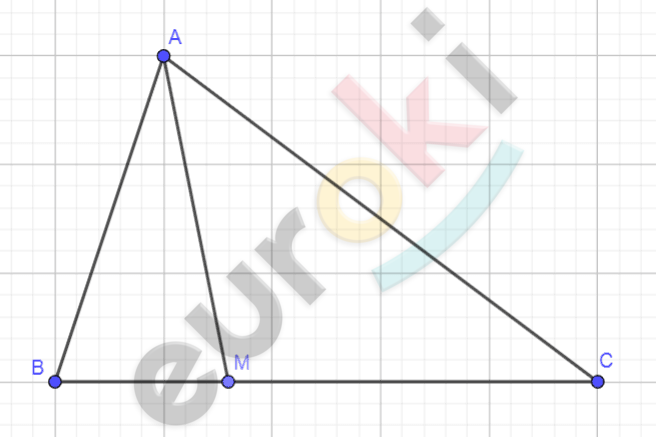
\[\mathbf{Дано:}\]

\[\mathrm{\Delta}ABC;\]

\[M \in BC;\]

\[AC > AB.\]

\[\mathbf{Доказать:}\]

\[AM < AC.\]

\[\mathbf{Доказательство.}\]

\[1)\ AC > AB\ (по\ условию),\ поэтому\ в\ в\ \mathrm{\Delta}ABC:\ \]

\[\angle B > \angle C\ (так\ как\ напротив\ большей\ стороны\ лежит\ больший\ угол).\]

\[2)\ \angle AMC - внешний\ к\ треугольнику\ ABM:\]

\[\angle AMC = \angle B + \angle BAM;\ \]

\[\angle B > \angle C.\]

\[Отсюда:\]

\[\angle AMC > \angle C\]

\[Следовательно\ в\ \mathrm{\Delta}AMC:\]

\[AM < AC\]

\[(так\ как\ напротив\ большего\ угла\ лежит\ большая\ сторона).\]

\[Что\ и\ требовалось\ доказать.\]