Решебник по геометрии 7 класс Атанасян ФГОС Задание 312

 

\[\boxed{\mathbf{312.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[\mathrm{\Delta}ABC;\]

\[M \in BC;\]

\[AC > AB.\]

\[\mathbf{Доказать:}\]

\[AM < AC.\]

\[\mathbf{Доказательство.}\]

\[1)\ AC > AB\ (по\ условию),\ \]

\[поэтому\ в\ в\ \mathrm{\Delta}ABC:\ \]

\[2)\ \angle AMC - внешний\ к\ \]

\[треугольнику\ ABM:\]

\[\angle AMC = \angle B + \angle BAM;\ \]

\[\angle B > \angle C.\]

\[Отсюда:\]

\[\angle AMC > \angle C\]

\[Следовательно\ в\ \mathrm{\Delta}AMC:\]

\[AM < AC\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{312.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи:\]

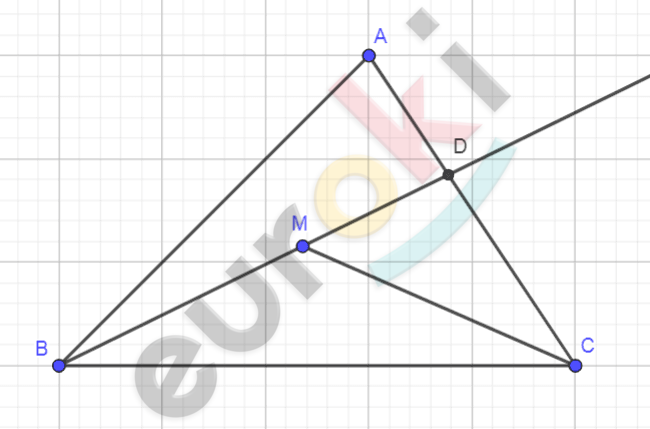
\[\mathbf{Дано:}\]

\[\mathrm{\Delta}ABC;\]

\[M \in ABC.\]

\[\mathbf{Доказать:}\]

\[MB + MC < AB + AC.\]

\[\mathbf{Доказательство.}\]

\[1)\ В\ треугольнике\ MDC:\]

\[MC < MD + DC\ (по\ неравенству\ треугольника).\]

\[2)\ В\ треугольнике\ ADB:\]

\[BD < AB + AD\ (по\ неравенству\ треугольника).\]

\[А\ еще:\]

\[BD = BM + MD\]

\[BM + MD < AB + AD.\]

\[3) + \frac{MC < MD + DC}{BM + MD < AB + AD\ \ \ \ \ \ \ \ \ \ \ \ } =\]

\[= MC + BM < DC + AB + AD;\ \]

\[AD + DC = AC;\]

\[получаем:\ \]

\[MC + MB < AC + AB.\]

\[Что\ и\ требовалось\ доказать.\]