Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 311
Задание 311
\[\boxed{\mathbf{311.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[Дано:\]
\[a \cap b = O.\]
\[Найти:\]
\[множество\ всех\ точек,\ \]
\[равноудаленных\ от\ \text{a\ }и\ \text{b.}\]
\[Решение.\]
\[1)\ Проведем\ биссектрисы\ \]
\[углов,\ образованных\ прямыми\ \]
\[\text{a\ }и\ b,обозначим\ их\ как\ \text{c\ }и\ \text{d.}\]
\[2)\ На\ прямой\ \text{d\ }отметим\ \]
\[случайную\ точку\ A,\ проведем\ \]
\[от\ нее\ высоты\ AA_{1}\ и\ AA_{2}\ к\ \]
\[прямым\ \text{a\ }и\ \text{b\ }соответственно.\]
\[3)\ Рассмотрим\ \mathrm{\Delta}AA_{1}\text{O\ }и\ \]
\[\mathrm{\Delta}AA_{2}O - прямоугольные:\]
\[\angle AOA_{2} = \angle AOA_{1}\ \]
\[(так\ как\ d - биссектриса);\ \]
\[OA - общий\ катет;\]
\[\mathrm{\Delta}AA_{1}O = \mathrm{\Delta}AA_{2}\text{O\ }\]
\[(по\ катету\ и\ прилежащему\ углу).\]
\[Получаем:\]
\[AA_{1} = AA_{2}.\]
\[3)\ На\ прямой\ \text{c\ }отметим\ \]
\[случайную\ точку\ B,\ проведем\ \]
\[от\ нее\ высоты\ BB_{1}\ и\ BB_{2}\ к\ \]
\[прямым\ \text{a\ }и\ \text{b\ }соответственно.\]
\[3)\ Рассмотрим\ \mathrm{\Delta}BB_{1}\text{O\ }и\ \]
\[\mathrm{\Delta}BB_{2}O - прямоугольные:\]
\[\angle BOB_{2} = \angle BOB_{1}\ \]
\[(так\ как\ c - биссектриса);\ \]
\[OB - общий\ катет.\]
\[\mathrm{\Delta}BB_{1}O = \mathrm{\Delta}BB_{2}\text{O\ }\]
\[(по\ катету\ и\ прилежащему\ углу).\]
\[Получаем:\]
\[BB_{1} = BB_{2}.\]
\[4)\ Следовательно,\ множеством\ \]
\[точек,\ равноудаленных\ от\ двух\]
\[пересекающихся\ прямых,\ \]
\[являются\ биссектриссы\ этих\ \]
\[углов.\]
\[\boxed{\mathbf{311.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
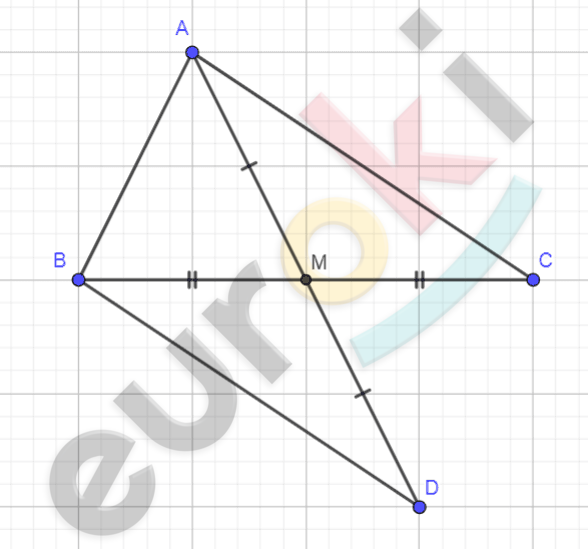
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
\[AM - медиана.\]
\[\mathbf{Доказать:}\]
\[AM < \frac{AB + AC}{2}.\]
\[\mathbf{Доказательство.}\]
\[1)\ На\ продолжении\ медианы\ AM\ отложим\ от\ точки\ \text{M\ }отрезок\ \]
\[MD = AM.\]
\[2)\ \mathrm{\Delta}AMC = \mathrm{\Delta}BMD - по\ двум\ сторонам\ и\ углу\ между\ ними:\]
\[\angle AMC = \angle BMD\ (как\ вертикальные);\ \]
\[AM = MD\ (по\ построению);\]
\[BM = MC.\]
\[Отсюда:\ \]
\[AC = BD.\ \]
\[3)\ Рассмотрим\ \mathrm{\Delta}ABD:\]
\[AD < AB + BD\ (по\ неравенству\ треугольника);\]
\[AD = AM + MD = 2AM\ (по\ построению);\]
\[AC = BD \Longrightarrow \ AB + BD = AB + AC.\]
\[2AM < AB + AC \Longrightarrow AM < \frac{AB + AC}{2}.\]
\[Что\ и\ требовалось\ доказать.\]
