Решебник по геометрии 7 класс Атанасян ФГОС Задание 280

 

\[\boxed{\mathbf{280.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[Найти:\]

\[множество\ всех\ точек\ внутри\ \]

\[\angle ABC,\ удаленных\ от\ BC\ на\ \]

\[расстояние\ \text{QP.}\]

\[Решение.\]

\[1)\ \]

\[2)\ По\ аксиоме\ параллельных\ \]

\[прямых\ через\ точку\ \text{Q\ }\]

\[проходит\ единственная\ \]

\[прямая,\ параллельная\ \text{BC.}\]

\[3)\ Все\ точки\ луча\ \text{OQ\ }\]

\[равноудаленны\ от\ точек\ луча\ \]

\[BC\ (по\ свойству\ \]

\[равноудаленных\ точек\ \]

\[параллельных\ прямых).\]

\[Вывод:луч\ \text{OQ\ }является\ \]

\[искомым\ множеством\ точек.\]

\[\text{\ \ }\]

\[\boxed{\mathbf{280.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи:\]

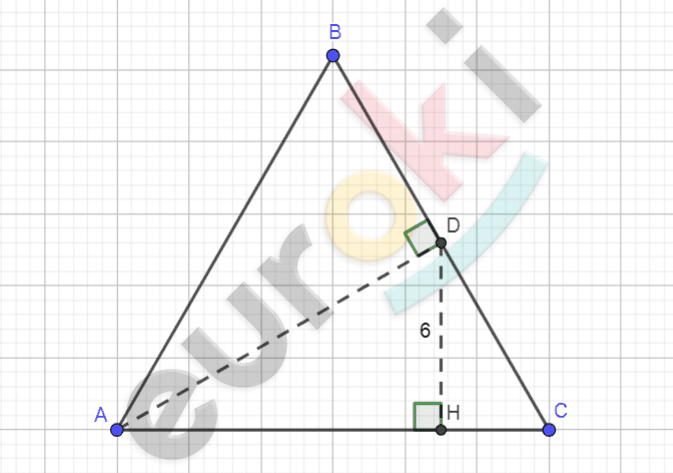
\[\mathbf{Дано:}\]

\[\mathrm{\Delta}ABC - равносторонний;\]

\[AD - бисс\ \angle A;\]

\[DH\bot AC;\]

\[DH = 6\ см.\]

\[\mathbf{Найти:}\]

\[AD - ?\]

\[\mathbf{Решение.}\]

\[1)\ \mathrm{\Delta}ABC - равносторонний:\]

\[\angle A = \angle B = \angle C = 60{^\circ};\]

\[AB = BC = AC.\]

\[2)\ \mathrm{\Delta}DHA - прямоугольный\ \]

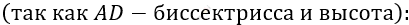
\[\mathbf{Ответ:}AD = 12\mathbf{\ }\mathbf{см}\mathbf{.}\]