Решебник по геометрии 7 класс Атанасян ФГОС Задание 274

 

\[\boxed{\mathbf{274.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[\mathrm{\Delta}ABC - равнобедренный;\]

\[AD = DC;\]

\[DF\bot BC;\]

\[DE\bot AB.\]

\[\mathbf{Доказать:}\]

\[DF = DE.\]

\[\mathbf{Доказательство.}\]

\[1)\ \mathrm{\Delta}ABC - равнобедренный:\]

\[\angle A = \angle C\ (по\ свойству).\]

\[2)\ Прямоугольные\ \mathrm{\Delta}DEA =\]

\[= \mathrm{\Delta}DFC - по\ гипотенузе\ и\ \]

\[острому\ углу:\]

\[\angle A = \angle C\ (см.\ пункт\ 1);\ \]

\[AD = DC\ (по\ условию).\]

\[3)\ По\ свойству\ равных\ \]

\[треугольников:\]

\[DF = DE.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{274.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи:\]

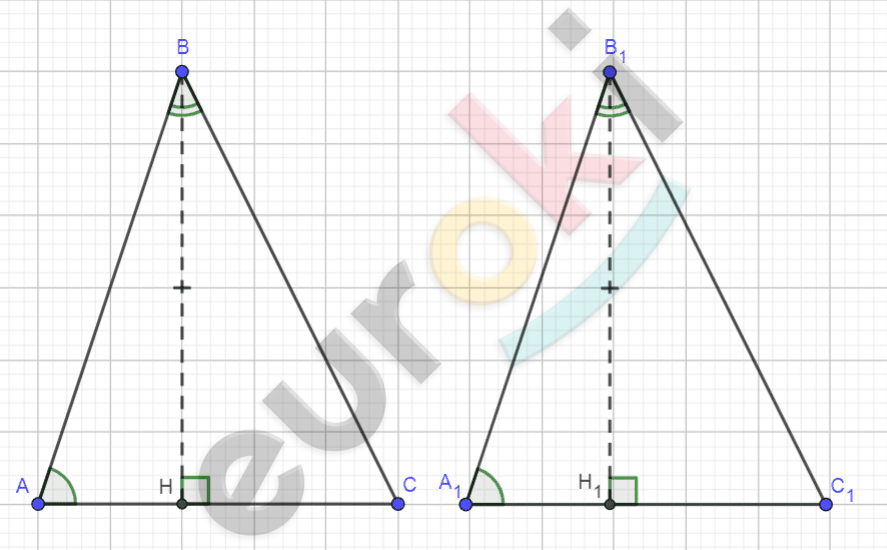
\[\mathbf{Дано:}\]

\[\mathrm{\Delta}\text{ABC\ }и\ \mathrm{\Delta}A_{1}B_{1}C_{1};\]

\[\angle A = \angle A_{1};\]

\[\angle B_{1} = \angle B;\]

\[BH = B_{1}H_{1} - высоты.\]

\[\mathbf{Доказать:}\]

\[\mathrm{\Delta}ABC = \mathrm{\Delta}A_{1}B_{1}C_{1}.\]

\[\mathbf{Доказательство.}\]

\[1)\ Прямоугольные\ \mathrm{\Delta}ABH =\]

\[= \mathrm{\Delta}A_{1}B_{1}H_{1} - по\ катету\ и\ \]

\[противолежащему\]

\[углц:\]

\[BH = B_{1}H_{1}\ (по\ условию);\]

\[\angle A = \angle A_{1}\ (по\ условию).\]

\[По\ свойству\ равных\ \]

\[треугольников:\]

\[AB = A_{1}B_{1}.\]

\[2)\ \mathrm{\Delta}ABC = \mathrm{\Delta}A_{1}B_{1}C_{1} - по\ \]

\[стороне\ и\ двум\ прилежащим\ \]

\[углам:\]

\[AB = A_{1}B_{1}\ (см.\ пункт\ 1);\ \]

\[\angle A = \angle A_{1}\ (по\ условию);\ \]

\[\angle B = \angle B_{1}\ (по\ условию).\]

\[Что\ и\ требовалось\ доказать.\]