Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 248
Задание 248
\[\boxed{\mathbf{248.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[\textbf{а)}\ AB = 1\ м;BC = 2\ м;\]
\[AC = 3\ м.\]
\[Используем\ неравенство\ \]
\[сторон\ треугольника:\]
\[AB < BC + AC \Longrightarrow 1 < 2 + 3 \Longrightarrow\]
\[\Longrightarrow 1 < 5 - верно;\]
\[BC < AB + AC \Longrightarrow 2 < 1 + 3 \Longrightarrow\]
\[\Longrightarrow 2 < 4 - верно;\]
\[AC < AB + BC \Longrightarrow 3 < 1 + 2 \Longrightarrow\]
\[\Longrightarrow 3 < 3 - неверно.\]
\[\mathrm{\Delta}ABC\ с\ данными\ сторонами\ не\ \]
\[существует.\]
\[\textbf{б)}\ AB = 1,2\ дм;BC = 1\ дм;\]
\[AC = 2,4\ дм.\]
\[Используем\ неравенство\ \]
\[сторон\ треугольника:\]
\[AB < BC + AC \Longrightarrow\]
\[\Longrightarrow 1,2 < 1 + 2,4 \Longrightarrow\]
\[\Longrightarrow 1,2 < 3,4 - верно;\]
\[BC < AB + AC \Longrightarrow\]
\[\Longrightarrow 1 < 1,2 + 2,4 \Longrightarrow\]
\[\Longrightarrow 1 < 3,6 - верно;\]
\[AC < AB + BC \Longrightarrow\]
\[\Longrightarrow 2,4 < 1,2 + 1 \Longrightarrow\]
\[\Longrightarrow 2,4 < 2,2 - неверно.\]
\[\mathrm{\Delta}ABC\ с\ данными\ сторонами\ \]
\[не\ существует.\]
\[Ответ:а)\ не\ существует;\]
\[\textbf{б)}\ не\ существует.\]
\[\boxed{\mathbf{248.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
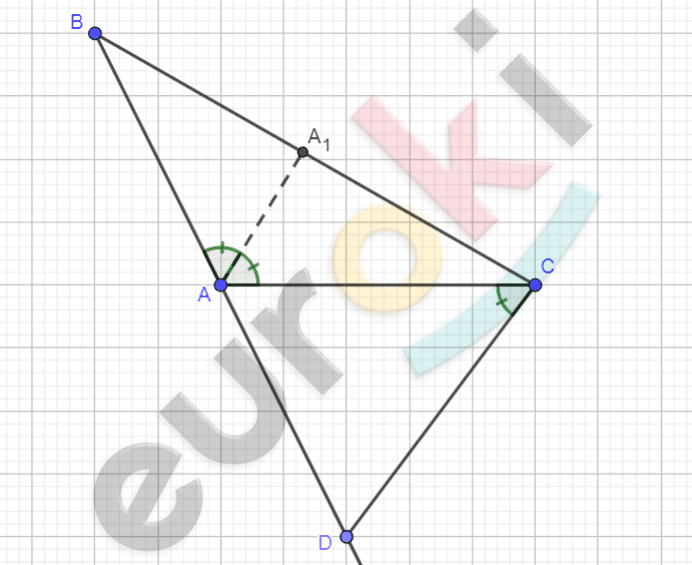
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}\text{ABC};\]
\[AA_{1} - бисс\ \angle A;\]
\[\text{CD} \parallel AA_{1};\]
\[\text{CD} \cap \text{BA} = D.\]
\[\mathbf{Доказать:}\]
\[AC = AD.\]
\[\mathbf{Доказательство.}\]
\[1)\ Рассмотрим\ AA_{1} \parallel CD\ и\ \]
\[AC - секущая:\]
\[\angle A_{1}AC = \angle ACD\ \]
\[(как\ накрестлежащие).\]
\[2)\ Рассмотрим\ \text{\ A}A_{1} \parallel CD\ и\ \]
\[AD - секущая:\]
\[\angle BAA_{1} = \angle ADC\ \]
\[(как\ соответственные).\]
\[3)\ \angle A_{1}AC = \angle ACD\ \]
\[(см.\ пункт\ 1);\ \]
\[\angle BAA_{1} = \angle ADC\ (см.\ пункт\ 2);\]
\[\angle BAA_{1} = \angle A_{1}\text{AC\ }\]
\[\left( \ AA_{1} - биссектриса \right).\]
\[Значит:\]
\[\angle ACD = \angle ADC.\]
\[Следовательно:\ \]
\[\mathrm{\Delta}DAC - равнобедренный\ \]
\[(по\ признаку\ равнобедренного\]
\[\ треугольника).\]
\[4)\ Получаем:\ \ AD = AC.\]
\[Что\ и\ требовалось\ доказать.\]
