Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 247
Задание 247
\[\boxed{\mathbf{247.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[130.\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
\[AB = AC;\]
\[AP = AQ.\]
\[\mathbf{Доказать:}\]
\[\textbf{а)}\ \mathrm{\Delta}BOC - равнобедренный;\]
\[\textbf{б)}\ AH\bot BC;\]
\[BH = HC.\]
\[\mathbf{Доказательство.}\]
\[\textbf{а)}\]
\[1)\ \mathrm{\Delta}BPC = \mathrm{\Delta}BQC - по\ двум\ \]
\[сторонам\ и\ углу\ между\ ними:\]
\[BC - общая;\]
\[\angle B = \angle C\ \]
\[(\mathrm{\Delta}ABC - равнобедренный);\]
\[2)\ По\ определению\ равных\ \]
\[треугольников:\ \]
\[\angle CBQ = \angle PCB.\]
\[Следовательно,\ по\ признаку\ \]
\[равнобедренного\ \]
\[треугольника:\ \]
\[\mathrm{\Delta}BOC - равнобедренный.\]
\[Что\ и\ требовалось\ доказать.\]
\[\textbf{б)}\]
\[1)\ \mathrm{\Delta}BOC - равнобедренный:\]
\[BO = OC.\]
\[2)\ \mathrm{\Delta}BOA = \mathrm{\Delta}COA - по\ трем\ \]
\[сторонам:\]
\[AO - общая;\]
\[OC = BO\ (см.\ пункт\ а);\]
\[AC = AB\ (по\ условию).\text{\ \ }\]
\[По\ определению\ равных\ \]
\[треугольников:\]
\[\angle BAO = \angle OAC.\]
\[Следовательно:\]
\[AO - биссектриса\ \angle A\ в\ \mathrm{\Delta}\text{ABC.}\]
\[3)\ AO \cap BC = H;\ \]
\[AO - биссектриса;\ \ \]
\[\mathrm{\Delta}ABC - равнобедренный:\]
\[4)\ Следовательно:\]
\[AH\bot BC\ и\ BH = HC.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{247.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
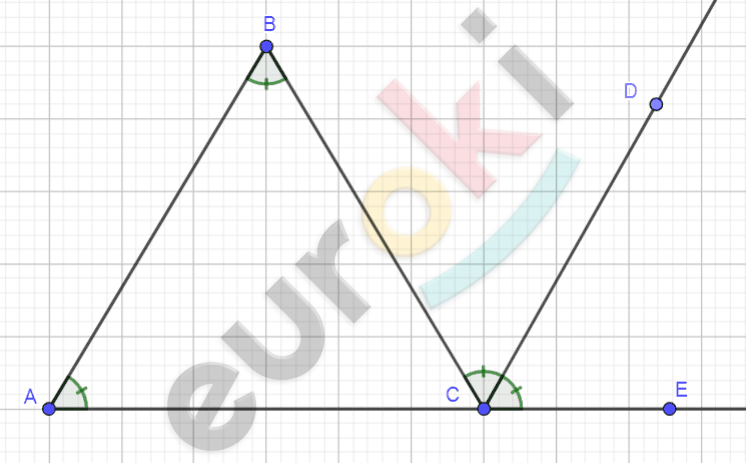
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}\text{ABC};\]
\[\text{CD} - бисс\ \angle\text{BCE};\]
\[\text{AB} \parallel \text{CD}.\]
\[\mathbf{Доказать:}\]
\[\mathrm{\Delta}\text{ABC} - равнобедренный.\]
\[\mathbf{Доказательство.}\]
\[1)\ Рассмотрим\ AB \parallel CD\ и\ \]
\[CB - секущая:\]
\[\angle DCB = \angle CBA\ \]
\[(как\ накрестлежащие).\]
\[2)\ Рассмотрим\ \ AB \parallel CD\ и\ \]
\[CA - секущая:\]
\[\angle BAC = \angle ECD\ \]
\[(как\ соответственные).\]
\[3)\ CD - биссектриса:\]
\[\angle DCB = \angle CBA;\]
\[\angle BAC = \angle ECD;\]
\[\angle BCD = \angle DCE.\]
\[Получаем:\]
\[\angle BAC = \angle CBA.\]
\[Следовательно,\ по\ признаку\ \]
\[равнобедренного\ \]
\[треугольника:\]
\[\mathrm{\Delta}ABC - равнобедренный.\ \]
\[Что\ и\ требовалось\ доказать.\]
