Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 242
Задание 242
\[\boxed{\mathbf{242.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
\[CD - бисс\ \angle BCE;\]
\[AB \parallel CD.\]
\[\mathbf{Доказать:}\]
\[\mathrm{\Delta}ABC - равнобедренный.\]
\[\mathbf{Доказательство.}\]
\[1)\ Рассмотрим\ AB \parallel CD\ и\ \]
\[CB - секущая:\]
\[\angle DCB = \angle CBA\ \]
\[(как\ накрестлежащие).\]
\[2)\ Рассмотрим\ \ AB \parallel CD\ и\ \]
\[CA - секущая:\]
\[\angle BAC = \angle ECD\ \]
\[(как\ соответственные).\]
\[3)\ CD - биссектриса:\]
\[\angle DCB = \angle CBA;\]
\[\angle BAC = \angle ECD;\]
\[\angle BCD = \angle DCE.\]
\[Получаем:\]
\[\angle BAC = \angle CBA.\]
\[Следовательно,\ по\ признаку\ \]
\[равнобедренного\ \]
\[треугольника:\]
\[\mathrm{\Delta}ABC - равнобедренный.\ \]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{242.еуроки - ответы\ на\ пятёрку}}\]
\[\textbf{а)}\ Рисунок\ по\ условию\ задачи:\]
\[Дано:\]
\[\mathrm{\Delta}ABC;\ \]
\[\angle A > \angle B > \angle C.\]
\[Сравнить:\]
\[AB;BC;AC.\]
\[Решение.\]
\[1)\ Напротив\ \angle A\ лежит\]
\[сторона\ BC;\]
\[напротив\ \angle B\ лежит\ \]
\[сторона\ AC;\]
\[напротив\ \angle C\ лежит\ \]
\[сторона\ \text{AB.}\]
\[2)\ Напротив\ большего\ угла\ \]
\[лежит\ большая\ сторона:\]
\[\angle A > \angle B > \angle C.\]
\[Значит:\]
\[\ BC > AC > BA.\]
\[\mathbf{Ответ:\ }BC > AC > BA.\]
\[б\mathbf{)\ Рисунок\ по\ условию\ задачи:}\]
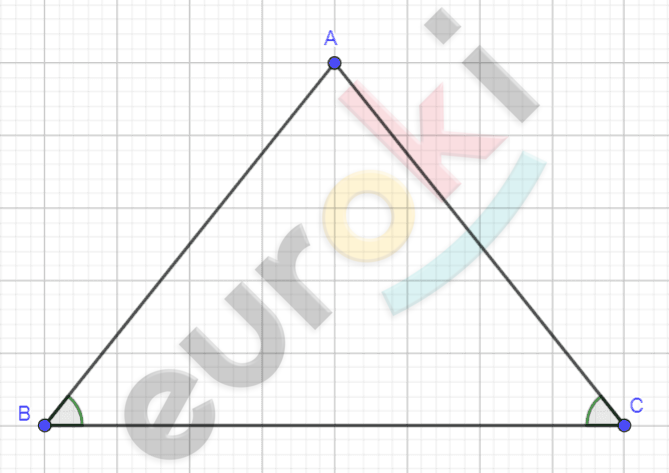
\[Дано:\]
\[\mathrm{\Delta}ABC;\ \]
\[\angle A > \angle B = \angle C.\]
\[Сравнить:\]
\[AB;BC;AC.\]
\[Решение.\]
\[1)\ Напротив\ \angle A\ лежит\ \]
\[сторона\ BC;\]
\[напротив\ \angle B\ лежит\ \]
\[сторона\ AC;\]
\[напротив\ \angle C\ лежит\ \]
\[сторона\ \text{AB.}\]
\[2)\ \angle B = \angle C:\ \]
\[\mathrm{\Delta}ABC - равнобедренный.\]
\[2)\ Напротив\ большего\ угла\ \]
\[лежит\ большая\ сторона:\]
\[\angle A > \angle B = \angle C.\]
\[Следовательно:\ \]
\[BC > AC = BA.\]
\[\mathbf{Ответ:\ }BC > AC = BA.\]
