Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 243
Задание 243
\[\boxed{\mathbf{243.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}\text{ABC};\]
\[AA_{1} - бисс\ \angle A;\]
\[\text{CD} \parallel AA_{1};\]
\[\text{CD} \cap \text{BA} = D.\]
\[\mathbf{Доказать:}\]
\[AC = AD.\]
\[\mathbf{Доказательство.}\]
\[1)\ Рассмотрим\ AA_{1} \parallel CD\ и\ \]
\[AC - секущая:\]
\[\angle A_{1}AC = \angle ACD\ \]
\[(как\ накрестлежащие).\]
\[2)\ Рассмотрим\ \text{\ A}A_{1} \parallel CD\ и\ \]
\[AD - секущая:\]
\[\angle BAA_{1} = \angle ADC\ \]
\[(как\ соответственные).\]
\[3)\ \angle A_{1}AC = \angle ACD\ \]
\[(см.\ пункт\ 1);\ \]
\[\angle BAA_{1} = \angle ADC\ (см.\ пункт\ 2);\]
\[\angle BAA_{1} = \angle A_{1}\text{AC\ }\]
\[\left( \ AA_{1} - биссектриса \right).\]
\[Значит:\]
\[\angle ACD = \angle ADC.\]
\[Следовательно:\ \]
\[\mathrm{\Delta}DAC - равнобедренный\ (по\ \]
\[признаку\ равнобедренного\]
\[\ треугольника).\]
\[4)\ Получаем:\ \ AD = AC.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{243.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ \ задачи:\]
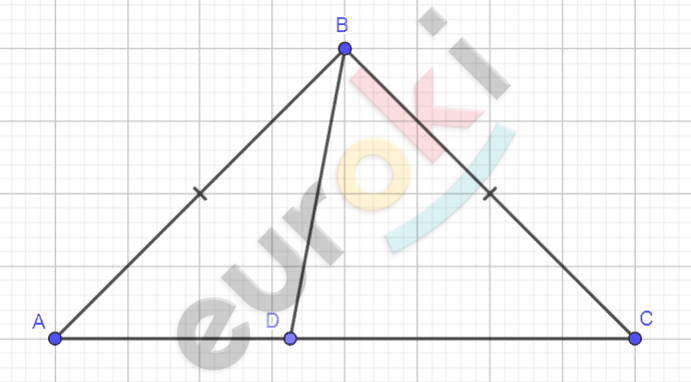
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC - равнобедренный;\ \]
\[D \in AC.\]
\[\mathbf{Доказать:}\]
\[BD < AB.\]
\[\mathbf{Доказательство.}\]
\[1)\ \mathrm{\Delta}ABC - равнобедренный:\]
\[\angle A = \angle C < 90{^\circ},\ так\ как\ \]
\[по\ теореме\ о\ сумме\ углов\]
\[в\ треугольнике\ два\ угла\ \]
\[не\ могут\ быть \geq 90{^\circ}.\]
\[2)\ \angle ADB\ и\ \angle BDC - смежные:\]
\[один\ угол\ тупой,\ \]
\[второй\ острый,\ либо\ оба\ угла\ \]
\[прямые.\]
\[3)\ Предположим,\ \]
\[что\ \angle ADB - тупой:\]
\[\angle ADB\ наибольший\ \]
\[в\ \mathrm{\Delta}ADB \rightarrow AB > BD.\]
\[4)\ Предположим,\ \]
\[что\ \angle BDC - тупой:\]
\[\angle BDC\ наибольший\ \]
\[в\ \mathrm{\Delta}BDC \rightarrow BC > BD.\]
\[5)\ Предположим,\ \]
\[что\ \angle ADB = \angle BDC = 90{^\circ}:\]
\[\mathrm{\Delta}ABD - прямоугольный,\ \]
\[BD - катет,\]
\[\ AB - гипотенуза \rightarrow AB > BD.\]
\[6)\ Следовательно,\ в\ любом\ \]
\[случае\ BD < AB.\]
\[Что\ и\ требовалось\ доказать.\]
