Решебник по геометрии 7 класс Атанасян ФГОС Задание 188

 

\[\boxed{\mathbf{188.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\(\ \)

\[\mathbf{Дано:}\]

\[AB \cap CD = O;\]

\[AO = OB;\]

\[CO = OD.\]

\[\mathbf{Доказать:}\]

\[AC \parallel BD.\]

\[\mathbf{Доказательство:}\]

\[1)\ \mathrm{\Delta}ACO = \mathrm{\Delta}BDO - по\ двум\ \]

\[сторонам\ и\ углу\ между\ ними:\]

\[\angle COA = \angle BOD\ \]

\[(как\ вертикальные\ углы);\]

\[CO = OD\ (по\ условию);\]

\[AO = OB\ (по\ условию).\]

\[Получаем:\]

\[\angle B = \angle A.\]

\[2)\ \angle A = \angle B - как\ накрест\ \]

\[лежащие\ углы\ при\ прямых\ \]

\[AC;BD\ и\ секущей\ \text{AB}\text{.\ }\]

\[По\ признаку\ параллельности\ \]

\[прямых:\]

\[AC \parallel BD.\]

\[Что\ и\ требовалось\ доказать.\ \ \]

\[\boxed{\mathbf{188.еуроки - ответы\ на\ пятёрку}}\]

\[Дано:\]

\[окружность\ (O;r);\]

\[( \cdot )\text{A\ }и\ ( \cdot )B;\ \ \]

\[отрезок\ \text{PQ.}\]

\[Построить:\ \]

\[\mathrm{\Delta}ABC;чтобы\ C \in окружности;\ \]

\[AC = PQ.\ \]

\[Построение.\]

\[1)\ Построим\ еще\ одну\ \]

\[окружность\ (A;PQ),\ чтобы\ они\ \]

\[пересеклись\ в\ точке\ C.\ \]

\[Соединим\ точки\ A;B;\]

\[C - и\ получим\ искомый\ \]

\[треугольник.\]

\[2)\ В\ данной\ задаче\ может\ \]

\[быть\ 2\ решения,\ ни\ одного\ \]

\[решения\ или\ 1\ решение.\ \]

\[Рассмотрим.\ \]

\[І\ случай - 2\ решения.\]

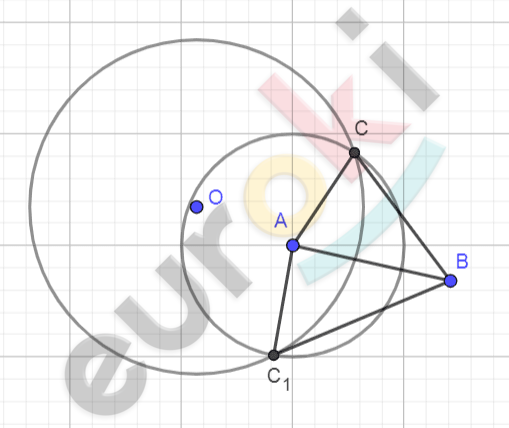
\[\mathrm{\Delta}ACB\ и\ \mathrm{\Delta}ABC_{1}.\]

\[ІІ\ случай - 1\ решение\ или\ \]

\[0\ решений.\]

\[Либо\ \mathrm{\Delta}AB_{1}C,\ \]

\(либо\ нет\ решений.\)