Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 146
Задание 146
\[\boxed{\mathbf{146.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\mathbf{\ задачи:}\]
\[\mathbf{Дано:}\]
\[Окружность\ (O;r);\]
\[\text{AB} = \text{CD} - диаметры;\]
\[CB = 13\ см;\]
\[\text{AB} = 16\ см.\]
\[\mathbf{Найти:}\]
\[P_{\text{AOD}} = ?\]
\[\mathbf{Решение.}\]
\[1)\ По\ построению:\]
\[AO = OB = OC = OD = r.\]
\[2)\ AB = AO + OB = 2OB =\]
\[= 2AO = 16;\]
\[AO = OB = 8\ см;\]
\[DO = OC = 8\ см.\]
\[3)\ \mathrm{\Delta}AOD = \mathrm{\Delta}COB - по\ двум\ \]
\[сторонам\ и\ углу\ между\ ними:\ \]
\[AO = OB\ (см.\ пункт\ 1);\]
\[DO = OC\ (см.\ пункт\ 1);\]
\[\angle AOD = \angle COB\ \]
\[(как\ вертикальные\ углы).\]
\[Значит:\ \]
\[AD = CB = 13\ см.\]
\[4)\ P_{\text{AOD}} = AO + OD + AD =\]
\[= 8 + 8 + 13 = 29\ см.\]
\[Ответ:P_{\text{AOD}} = 29\ см.\]
\[\boxed{\mathbf{146.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ \mathbf{задачи:}\]
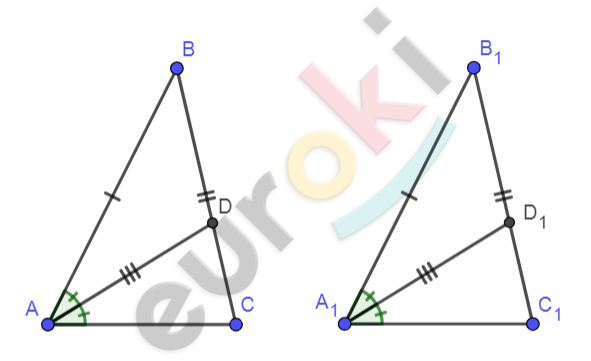
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\ \mathrm{\Delta}A_{1}B_{1}C_{1};\]
\[AD;A_{1}D_{1} - биссектрисы;\]
\[AB = A_{1}B_{1};\ \ \]
\[BD = B_{1}D_{1};\]
\[AD = A_{1}D_{1}.\]
\[\mathbf{Доказать:}\]
\[\mathrm{\Delta}ABC = \mathrm{\Delta}A_{1}B_{1}C_{1}.\]
\[\mathbf{Доказательство.}\ \]
\[1)\ Сначала\ рассмотирим\ \]
\[треугольники\ \]
\[1)\ \mathrm{\Delta}ABD = \mathrm{\Delta}A_{1}B_{1}D_{1} - \ по\ трем\ \]
\[сторонам:\]
\[AB = A_{1}B_{1}\ (по\ условию);\ \ \]
\[AD = A_{1}D_{1}\ (по\ условию);\ \ \]
\[BD = B_{1}D_{1}\ (по\ условию).\]
\[Значит:\]
\[\angle BAD = \angle B_{1}A_{1}D_{1};\ \ \ \]
\[\angle B = \angle B_{1}.\]
\[2)\ \angle A = \angle A_{1};\ \ потому\ что:\]
\[\angle A = \angle BAD + \angle DAC;\]
\[\angle A_{1} = \angle B_{1}A_{1}D_{1} + \angle D_{1}A_{1}C_{1};\]
\[AD;A_{1}D_{1} - по\ условию,\ \]
\[биссектрисы.\]
\[3)\ \mathrm{\Delta}ABC = \mathrm{\Delta}A_{1}B_{1}C_{1} -\]
\[по\ стороне\ и\ двум\ \]
\[прилежащим\ к\ ней\ углам:\]
\[\angle B = \angle B_{1}\ (см.\ пункт\ 1);\]
\[\angle A = \angle A_{1}\ (см.\ пункт\ 2);\]
\[AB = A_{1}B_{1}(по\ условию).\]
\[Что\ и\ требовалось\ доказать.\]
