Решебник по геометрии 7 класс Атанасян ФГОС Задание 1426

\[\boxed{\mathbf{1426.еуроки - ответы\ на\ пятёрку}}\]

\[\mathbf{Дано:}\]

\[a - сторона\ ромба;\]

\[m;n - диагонали.\]

\[Построить:\]

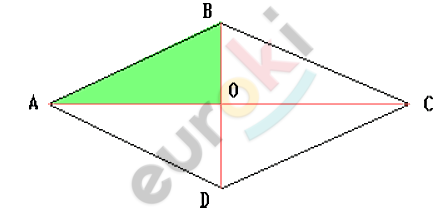
\[ромб.\]

\[\mathbf{Построение.}\]

\[Задача\ сводится\ к\ построению\ \]

\[прямоугольного\ треугольника\ \]

\[\text{AOB},\ по\ гипотенузе\ и\ данному\ \]

\[отношению\ катетов.\]

\[1)\ Построим\ прямой\ угол\ \text{O.}\]

\[2)\ Отметим\ на\ одной\ стороне\ \]

\[угла\ O\ отрезок\ OA_{1},\ равный\ m,\ \]

\[а\ на\ другой - \ отрезок\ OB_{1},\]

\[\ равный\ \text{n.}\]

\[3)\ Проведем\ прямую\ A_{1}B_{1}\ \]

\[и\ отметим\ на\ ней\ отрезок\ \]

\[A_{1}A_{2},\ проходящий\ через\ \]

\[точку\ B_{1}\ и\ равный\ \text{AB.}\]

\[4)\ Через\ точку\ B_{2}\ проведем\ \]

\[прямую,\ параллельную\ OA_{1},\ \]

\[на\ пересечении\ данной\ \]

\[прямой\ и\ OB_{1}\ отметим\ точку\ \]

\[\text{B.}\]

\[5)\ Через\ точку\ \text{B\ }проведем\ \]

\[прямую,\ параллельную\ A_{1}B_{1},\ \]

\[на\ пересечении\ данной\ \]

\[прямой\ и\ OA_{1}\ отметим\ точку\ \text{A.}\]

\[6)\ Соединим\ точки\ A,\ B\ и\ \text{O.}\]

\[7)\ Достроим\ треугольник\ \]

\[до\ ромба\ ABCD,\ со\ стороной\ \]

\[AB = a.\]