Решебник по геометрии 7 класс Атанасян ФГОС Задание 1425

\[\boxed{\mathbf{1425.еуроки - ответы\ на\ пятёрку}}\]

\[Задача\ сводится\ к\ построению\ \]

\[прямоугольного\ треугольника\ \]

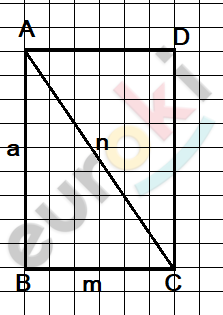
\[по\ гипотенузе = n\ и\ \]

\[катету = \text{m.}\]

\[1)\ Пусть\ даны\ отрезок\ n,\ \]

\[равный\ гипотенузе,\ и\ отрезок\ \]

\[m,\ равный\ катету\ (n > m).\]

\[2)\ На\ произвольной\ прямой\ \]

\[отложим\ отрезок\ BC,\ \]

\[равный\ m.\]

\[3)\ Из\ точки\ \text{B\ }проведем\ \]

\[окружность\ произвольного\ \]

\[радиуса.\]

\[4)\ Из\ точек\ пересечения\ этой\ \]

\[окружности\ и\ прямой\ \]

\[проведем\ две\ окружности\ \]

\[одинакового\ радиуса.\]

\[5)\ Через\ точки\ пересечения\ \]

\[этих\ окружностей\ проведем\ \]

\[вторую\ прямую,\ она\ \]

\[перпендикулярна\ первой\ \]

\[прямой.\]

\[6)\ Из\ точки\ \text{C\ }проведем\ \]

\[окружность\ радиуса\ n,\ \]

\[на\ пересечении\ этой\]

\[окружности\ и\ второй\ прямой\ \]

\[отметим\ точку\ \text{A.}\]

\[7)\ Треугольник\ ABC -\]

\[искомый.\]

\[2)\ Достроим\ его\ \]

\[до\ прямоугольника.\]

\[3)\ Прямоугольник\ ABCD -\]

\[искомый.\]