Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 1139
Задание 1139
\[\boxed{\mathbf{1139.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[v = 4\ км/ч;\]
\[t_{обхода} = t_{перес} + \ 45\ мин.\]
\[\mathbf{Найти:}\]
\[C - ?\]
\[\mathbf{Решение.}\]
\[1)\ Пусть\ \text{t\ }минут - нужно\ для\ \]
\[пересечения:\]
\[(t + 45)\ минут - нужно\ для\ \]
\[обхода.\]
\[2)\ v \bullet t = d - расстояние\ при\ \]
\[пересечении.\]
\[3)\ v \bullet (t + 45) = C - расстояние\ \]
\[при\ обходе.\]
\[4)\ vt = 2R\ и\ vt + 45v = 2\pi R:\]
\[2R + 45v = 2\pi R.\]
\[5)\ 45\ мин = \frac{45}{60} = \frac{3}{4}\ ч\]
\[2R + \frac{3}{4} \bullet 4 = 2\pi R\]
\[2R - 2\pi R + 3 = 0\]
\[2R(1 - \pi) = - 3\]
\[R = \frac{- 3}{2(1 - 3,14)} = 0,7\ км.\]
\[6)\ C = 2\pi R = 2 \bullet 3,14 \bullet 0,7 =\]
\[= 4,4\ км.\]
\[Ответ:длина\ опушки\ \]
\[равна\ 4,4\ км.\]
\[\boxed{\mathbf{1139.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунки\ по\ условию\ задачи:\]
\[\mathbf{а)}\]
\(\mathbf{\ }\)
\[\mathbf{б)\ }\]
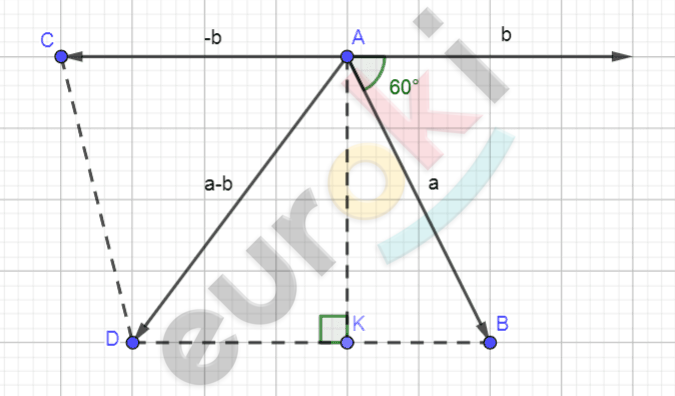
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
\[\left| \overrightarrow{a} \right| = 5;\]
\[\left| \overrightarrow{b} \right| = 8;\]
\[\widehat{\overrightarrow{a}\overrightarrow{b}} = 60{^\circ}.\]
\[\mathbf{Найти:}\]
\[\textbf{а)}\left| \overrightarrow{a} + \overrightarrow{b} \right| - ?;\]
\[\textbf{б)}\left| \overrightarrow{a} - \overrightarrow{b} \right| - ?\]
\[\mathbf{Решение.}\]
\[\textbf{а)}\ 1)\ \mathrm{\Delta}ADK\ и\ \mathrm{\Delta}ACK -\]
\[прямоугольные:\]
\[\angle KAD = 90{^\circ} - 60{^\circ} = 30{^\circ};\]
\[KD = \frac{1}{2}AD = \frac{1}{2} \bullet 5 = 2,5.\]
\[2)\ KC = KD + DC = 2,5 + 8 =\]
\[= 10,5\ \left( AB = DC = \overrightarrow{b} \right).\]
\[3)\ \left. \ \frac{AK = \sqrt{AD^{2} - KD^{2}}}{AK = \sqrt{AC^{2} - CK^{2}}} \right| \Longrightarrow\]
\[\Longrightarrow AD^{2} - KD^{2} = AC^{2} - CK^{2}.\]
\[25 - 6,25 = AC^{2} - 110,25\]
\[AC^{2} = 110,25 + 25 - 6,25 =\]
\[= 129\]
\[AC = \sqrt{129}.\]
\[\left| \overrightarrow{a} + \overrightarrow{b} \right| = \sqrt{129}.\]
\[\textbf{б)}\ 1)\ \mathrm{\Delta}AKB\ и\ \mathrm{\Delta}AKD -\]
\[прямоугольные:\]
\[\angle KAB = 90{^\circ} - 60{^\circ} = 30{^\circ};\]
\[KB = \frac{1}{2}AB = \frac{1}{2} \bullet 5 = 2,5.\]
\[2)\ DB = DK + KB = 8\]
\[DK = 8 - 2,5 = 5,5.\]
\[3)\ \left. \ \frac{AK = \sqrt{AB^{2} - KB^{2}}}{AK = \sqrt{AD^{2} - DK^{2}}} \right| \Longrightarrow\]
\[\Longrightarrow AB^{2} - KB^{2} = AD^{2} - DK^{2};\]
\[25 - 6,25 = AD^{2} - 30,25\]
\[AD^{2} = 25 - 6,25 + 30,25 = 49\]
\[AD = \sqrt{49} = 7\]
\[\left| \overrightarrow{a} - \overrightarrow{b} \right| = 7.\]
\[\mathbf{Ответ:}а)\ \sqrt{129};б)\ 7.\]
