Решебник по геометрии 7 класс Атанасян ФГОС Задание 1115

 

\[\boxed{\mathbf{1115.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Формула:\]

\[S = \pi R^{2}.\]

\[\textbf{а)}\ R_{1} = kR \Longrightarrow S_{1} = \pi\left( \text{kR} \right)^{2} =\]

\[= k^{2}\pi R^{2}:\]

\[\frac{S_{1}}{S} = \frac{k^{2}\pi R^{2}}{\pi R^{2}} = k^{2} - раз\ \]

\[\left( увеличится\ в\ \text{k\ }раз \right);\]

\[\textbf{б)}\ R_{2} = \frac{R}{k} \Longrightarrow S_{2} = \pi\left( \frac{R}{k} \right)^{2} =\]

\[= \frac{\pi R^{2}}{k^{2}};\]

\[\frac{S_{2}}{S} = \frac{\pi R^{2}}{k^{2}\pi R^{2}} = \frac{1}{k^{2}} - раз\ \]

\[\left( уменьшится\ в\ \text{k\ }раз \right).\]

\[Ответ:а)\ увеличится\ в\ \text{k\ }раз;\]

\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ б)\ уменьшится\ в\ \text{k\ }раз.\]

\[\boxed{\mathbf{1115.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи:\]

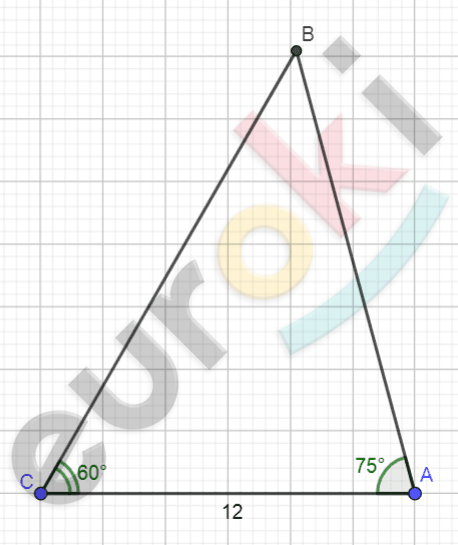
\[\mathbf{Дано:}\]

\[\mathrm{\Delta}ABC;\]

\[AC = 12\ см;\]

\[\angle A = 75{^\circ};\]

\[\angle C = 60{^\circ}.\]

\[\mathbf{Найти:}\]

\[AB - ?\]

\[S_{\text{ABC}} - ?\]

\[\mathbf{Решение.}\]

\[1)\ \angle B = 180{^\circ} - (\angle A + \angle C) =\]

\[= 45{^\circ}.\]

\[2)\ По\ теоремме\ синусов:\]

\[\frac{12}{\sin{45{^\circ}}} = \frac{\text{AB}}{\sin{60{^\circ}}}\]

\[AB = \frac{12\sin{60{^\circ}}}{\sin{45{^\circ}}} =\]

\[= \left( 12 \bullet \frac{\sqrt{3}}{2} \right)\ :\frac{\sqrt{2}}{2} = 6\sqrt{3} \bullet \frac{2}{\sqrt{2}} =\]

\[= \frac{12\sqrt{3}}{\sqrt{2}} = \frac{12\sqrt{6}}{2} = 6\sqrt{6}\ см.\]

\[3)\ S_{\text{ABC}} = \frac{1}{2} \bullet AB \bullet AC \bullet \sin{75{^\circ}} =\]

\[= \frac{1}{2} \bullet 12 \bullet 6\sqrt{6} \bullet 0,96 \approx 85,2\ см^{2}.\]

\[Ответ:S_{\text{ABC}} = 85,2\ см^{2};\ \]

\[AB = 6\sqrt{6}\ см.\]