Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 1114
Задание 1114
\[\boxed{\mathbf{1114.ОК\ ГДЗ - домашка\ на}\ 5}\]
| \[S\] | \[12,56\] | \[78,5\] | \[9\] | \[0,26\] | \[49\pi\] | \[9258,26\] | \[9,42\] | \[6,25\] |
|---|---|---|---|---|---|---|---|---|
| \[R\] | \[2\] | \[5\] | \[1,69\] | \[\frac{2}{7}\] | \[7\] | \[54,3\] | \[\sqrt{3}\] | \[1,41\] |
\[Формула:\]
\[S = \pi R^{2}\ и\ R = \sqrt{\frac{S}{\pi}};где\ \pi = 3,14.\]
\[1)\ S = 3,14 \bullet 2^{2} = 3,14 \bullet 4 =\]
\[= 12,56;\]
\[2)\ S = 3,14 \bullet 5^{2} = 3,14 \bullet 25 =\]
\[= 78,5;\]
\[3)\ R = \sqrt{\frac{9}{3,14}} = 1,69;\]
\[4)\ S = 3,14 \bullet \left( \frac{2}{7} \right)^{2} = \frac{3,14 \bullet 4}{49} =\]
\[= 0,26;\]
\[5)\ R = \sqrt{\frac{49\pi}{\pi}} = \sqrt{49} = 7;\]
\[6)\ S = 3,14 \bullet {54,3}^{2} = 9258,26;\]
\[7)\ S = 3,14 \bullet {\sqrt{3}}^{2} = 3,14 \bullet 3 =\]
\[= 9,42;\]
\[8)\ R = \sqrt{\frac{6,25}{3,14}} = 1,41.\]
\[\boxed{\mathbf{1114.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
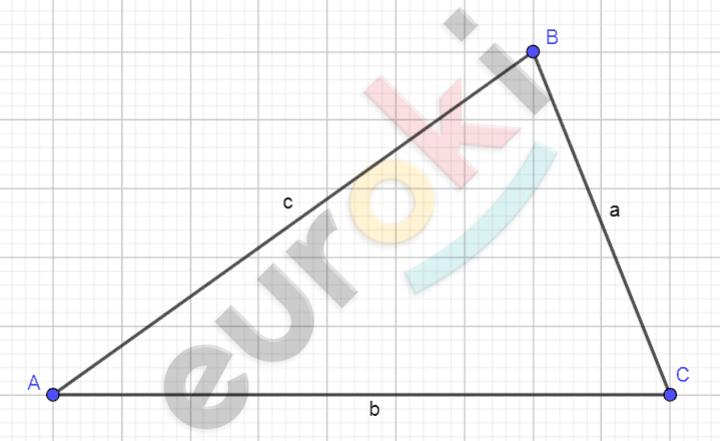
\[\textbf{а)}\ \angle A = 60{^\circ};\ \angle B = 40{^\circ};c = 14:\]
\[1)\ \angle C = 180{^\circ} - (60{^\circ} + 40{^\circ}) =\]
\[= 80{^\circ};\]
\[2)\ По\ теореме\ синусов:\]
\[\frac{\text{AB}}{\sin{\angle C}} = \frac{\text{BC}}{\sin{\angle A}} = \frac{\text{AC}}{\sin{\angle B}};\]
\[\frac{14}{\sin{80{^\circ}}} = \frac{a}{\sin{60{^\circ}}}\]
\[\frac{14}{0,9848} = \frac{a}{0,866} \Longrightarrow a = 12,31;\]
\[\frac{14}{\sin{80{^\circ}}} = \frac{b}{\sin{40{^\circ}}}\]
\[\frac{14}{0,9848} = \frac{b}{0,6428} \Longrightarrow b = 9,14.\ \]
\[\textbf{б)}\ \angle A = 30{^\circ};\ \angle C = 75{^\circ};\ b = 4,5:\]
\[1)\ \angle B = 180{^\circ} - (30{^\circ} + 75{^\circ}) =\]
\[= 75{^\circ}.\]
\[2)\ \angle B = \angle C \Longrightarrow \mathrm{\Delta}ABC -\]
\[равнобедренный:\]
\[\ c = b = 4,5.\]
\[3)\ По\ теореме\ синусов:\]
\[\frac{\text{AB}}{\sin{\angle C}} = \frac{\text{BC}}{\sin{\angle A}} = \frac{\text{AC}}{\sin{\angle B}}\]
\[\frac{a}{\sin{30{^\circ}}} = \frac{4,5}{\sin{75{^\circ}}}\]
\[\frac{a}{0,5} = \frac{4,5}{0,9659}\]
\[a = 2,33.\]
\[\textbf{в)}\ \angle A = 80{^\circ};a = 16;b = 10:\]
\[1)\ По\ теореме\ синусов:\]
\[\frac{\text{AB}}{\sin{\angle C}} = \frac{\text{BC}}{\sin{\angle A}} = \frac{\text{AC}}{\sin{\angle B}}\]
\[\frac{16}{\sin{80{^\circ}}} = \frac{10}{\sin{\angle B}}\]
\[\sin{\angle B} = \frac{10 \bullet 0,9848}{16} = 0,6155\]
\[\angle B = 37{^\circ}59^{'}.\]
\[2)\ \angle C =\]
\[= 180{^\circ} - \left( 80{^\circ} + 37{^\circ}59^{'} \right) =\]
\[= 62{^\circ}1^{'}.\]
\[3)\ \frac{16}{\sin{80{^\circ}}} = \frac{c}{\sin{61{^\circ}1^{'}}}\]
\[c = \frac{16 \bullet 0,8830}{0,9848}\]
\[c = 14,35.\]
\[\textbf{г)}\ \angle B = 45{^\circ};\ \angle C = 70{^\circ};\]
\[a = 24,6:\]
\[1)\ \angle A = 180{^\circ} - (45{^\circ} + 70{^\circ}) =\]
\[= 65{^\circ}.\]
\[2)\ По\ теореме\ синусов:\]
\[\frac{\text{AB}}{\sin{\angle C}} = \frac{\text{BC}}{\sin{\angle A}} = \frac{\text{AC}}{\sin{\angle B}}\]
\[\frac{24,6}{\sin{65{^\circ}}} = \frac{b}{\sin{45{^\circ}}}\]
\[\frac{24,6}{0,9063} = \frac{b}{0,7071}\]
\[b = 19,19.\]
\[\frac{24,6}{\sin{65{^\circ}}} = \frac{c}{\sin{70{^\circ}}}\]
\[\frac{24,6}{0,9063} = \frac{c}{0,9397}\]
\[c = 25,51.\]
\[\textbf{д)}\ \angle A = 60{^\circ};a = 10;b = 7:\]
\[1)\ По\ теореме\ синусов:\]
\[\frac{\text{AB}}{\sin{\angle C}} = \frac{\text{BC}}{\sin{\angle A}} = \frac{\text{AC}}{\sin{\angle B}}\]
\[\frac{10}{\sin{60{^\circ}}} = \frac{7}{\sin{\angle B}}\]
\[\sin{\angle B} = \frac{7 \bullet 0,8660}{10} = 0,6062\]
\[\angle B = 37{^\circ}19^{'}.\]
\[2)\ \angle C =\]
\[= 180{^\circ} - \left( 60{^\circ} + 37{^\circ}19^{'} \right) =\]
\[= 82{^\circ}41^{'}.\]
\[3)\ \frac{10}{\sin{60{^\circ}}} = \frac{c}{\sin{82{^\circ}41^{'}}}\]
\[c = \frac{10 \bullet 0,9919}{0,8660}\]
\[c = 11,45.\]
\[\textbf{е)}\ \angle C = 54{^\circ};a = 6,3;b = 6,3:\]
\[1)\ a = b \Longrightarrow \ \]
\[\Longrightarrow \mathrm{\Delta}ABC - равнобедренный:\]
\[\angle A = \angle B = (180{^\circ} - 54{^\circ}):2 =\]
\[= 63{^\circ}.\]
\[2)\ По\ теореме\ косинусов:\]
\[c^{2} = a^{2} + b^{2} - 2ab \bullet \cos{\angle C}\]
\[c^{2} = 79,38 - 79,38 \bullet 0,5878 =\]
\[= 32,72\]
\[c = 5,72.\]
\[\textbf{ж)}\ \angle A = 87{^\circ};c = 45;b = 32:\]
\[1)\ По\ теореме\ косинусов:\]
\[a^{2} = b^{2} + c^{2} - 2bc \bullet \cos{\angle A}\]
\[a^{2} =\]
\[= 1024 + 2025 - 2880 \bullet 0,0523 =\]
\[= 2898,38\]
\[a = 53,84.\]
\[2)\ По\ теореме\ синусов:\]
\[\frac{\text{AB}}{\sin{\angle C}} = \frac{\text{BC}}{\sin{\angle A}} = \frac{\text{AC}}{\sin{\angle B}}\]
\[\frac{53,84}{\sin{87{^\circ}}} = \frac{32}{\sin{\angle B}}\]
\[\sin{\angle B} = \frac{32 \bullet 0,9986}{53,84} = 0,5935\]
\[\angle B = 36{^\circ}24^{'}.\]
\[3)\ \angle C =\]
\[= 180{^\circ} - \left( 87{^\circ} + 36{^\circ}24^{'} \right) =\]
\[= 56{^\circ}36^{'}.\]
\[\textbf{з)}\ a = 14;b = 18;c = 20:\]
\[1)\ По\ теореме\ косинусов:\]
\[c^{2} = b^{2} + a^{2} - 2ab \bullet \cos{\angle C}\]
\[20^{2} = 18^{2} + 14^{2} - 2 \bullet 18 \bullet 14 \bullet \cos{\angle C}\]
\[400 = 324 + 196 - 504 \bullet \cos{\angle C}\]
\[504\cos{\angle C = 120}\]
\[\cos{\angle C} = 0,2381\]
\[\angle C = 76{^\circ}13^{'}.\]
\[2)\ По\ теореме\ косинусов:\]
\[b^{2} = a^{2} + c^{2} - 2ac \bullet \cos{\angle B}\]
\[18^{2} = 20^{2} + 14^{2} - 2 \bullet 20 \bullet 14 \bullet \cos{\angle B}\]
\[324 = 400 + 196 - 560 \bullet \cos{\angle B}\]
\[560\cos{\angle B = 272}\]
\[\cos{\angle B} = 0,4857\]
\[\angle B = 60{^\circ}57^{'}.\]
\[3)\ \angle A =\]
\[= 180{^\circ} - \left( 76{^\circ}13^{'} + 60{^\circ}57^{'} \right) =\]
\[= 42{^\circ}50^{'}.\]
\[\textbf{и)}\ a = 6;b = 7,3;c = 4,8:\]
\[1)\ По\ теореме\ косинусов:\]
\[c^{2} = b^{2} + a^{2} - 2ab \bullet \cos{\angle C}\]
\[{4,8}^{2} =\]
\[= {7,3}^{2} + 6^{2} - 2 \bullet 6 \bullet 7,3 \bullet \cos{\angle C}\]
\[23,04 =\]
\[= 53,29 + 36 - 87,6 \bullet \cos{\angle C}\]
\[87,6\cos{\angle C = 66,25}\]
\[\cos{\angle C} = 0,7563\]
\[\angle C = 40{^\circ}52^{'}.\]
\[2)\ По\ теореме\ косинусов:\]
\[b^{2} = a^{2} + c^{2} - 2ac \bullet \cos{\angle B}\]
\[{7,3}^{2} =\]
\[= 6^{2} + {4,8}^{2} - 2 \bullet 6 \bullet 4,8 \bullet \cos{\angle B}\]
\[53,29 =\]
\[= 36 + 23,04 - 57,6 \bullet \cos{\angle B}\]
\[57,6\cos{\angle B = 5,75}\]
\[\cos{\angle B} = 0,0998\]
\[\angle B = 84{^\circ}16^{'}.\]
\[3)\ \angle A =\]
\[= 180{^\circ} - \left( 84{^\circ}16^{'} + 40{^\circ}52^{'} \right) =\]
\[= 54{^\circ}52^{'}.\]
