Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 1090
Задание 1090
\[\boxed{\mathbf{1090.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\ \]
\[окружность\ (O;R);\]
\[AB = BC = AC;\]
\[AB = 3\ см.\]
\[\mathbf{Найти:}\]
\[d - ?\]
\[\mathbf{Решение.}\]
\[R = \frac{a\sqrt{3}}{3} = \frac{3\sqrt{3}}{3} = \sqrt{3}\ см.\]
\[d = 2R = 2\sqrt{3}\ см.\]
\[Ответ:\ d = 2\sqrt{3}\ см.\]
\[\boxed{\mathbf{1090.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
\[A( - 7;5);\]
\[B(3; - 1);\]
\[C(5;3).\]
\[\mathbf{Найти:}\]
\[уравнение\ прямых\]
\[\textbf{а)}\ AB;BC;AC;\]
\[\textbf{б)}\ серединных\ \]
\[перпендикуляров;\]
\[\textbf{в)}\ средних\ линий.\]
\[\mathbf{Решение.}\]
\[\textbf{а)}\ 1)\ AB:\ \]
\[\left\{ \begin{matrix} - 7a + 5b + c = 0 \\ 3a - b + c = 0\ \ \ \ \ \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} - 7a + 15a + 5c + c = 0 \\ b = 3a + c\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} 8a = - 6c\ \ \\ b = 3a + c \\ \end{matrix} \right.\ \text{\ \ \ }\]
\[\left\{ \begin{matrix} a = - \frac{3}{4}c \\ b = - \frac{5}{4}c \\ \end{matrix} \right.\ \]
\[\left. \ - \frac{3}{4}cx - \frac{5}{4}cy + c = 0\ \ \ \ \ \right|\left( - \frac{4}{c} \right)\]
\[2)\ BC:\ \]
\[\left\{ \begin{matrix} 3a - b + c = 0\ \ \\ 5a + 3b + c = 0 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} b = 3a + c\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 5a + 9a + 3c + c = 0 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} b = 3a + c \\ a = - \frac{2}{7}\text{c\ \ \ } \\ \end{matrix} \right.\ \text{\ \ \ }\]
\[\left\{ \begin{matrix} b = \frac{1}{7}\text{c\ \ \ \ } \\ a = - \frac{2}{7}c \\ \end{matrix} \right.\ \]
\[\left. \ - \frac{2}{7}cx + \frac{1}{7}cy + c = 0\ \ \ \ \ \ \right|\left( - \frac{7}{c} \right)\]
\[3)\ AC:\ \]
\[\left\{ \begin{matrix} - 7a + 5b + c = 0 \\ 5a + 3b + c = 0\ \ \ \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} 21a - 15b - 3c = 0 \\ 25a + 15b + 5c = 0 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} 46a = - 2c\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 21a - 15b - 3c = 0 \\ \end{matrix} \right.\ \text{\ \ \ }\]
\[\left\{ \begin{matrix} a = - \frac{1}{23}c \\ b = - \frac{6}{23}c \\ \end{matrix} \right.\ \]
\[\left. \ - \frac{1}{23}cx - \frac{6}{23}cy + c = 0\ \ \ \ \ \right|\left( - \frac{23}{c} \right)\]
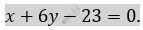
\[4)\ MN:\ \]
\[\left\{ \begin{matrix} - 2a + 2b + c = 0 \\ 4a + b + c = 0\ \ \ \ \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} 2a = 2b + c \\ b = - 4a - c \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} a = - \frac{1}{10}c \\ b = - \frac{6}{10}c \\ \end{matrix} \right.\ \text{\ \ \ }\]
\[\left. \ - \frac{1}{10}cx - \frac{6}{10}cy + c = 0\ \ \ \ \ \right| \cdot \left( - \frac{10}{c} \right)\]
\[5)\ NK:\ \]
\[\left\{ \begin{matrix} 4a + b + c = 0\ \ \ \\ - a + 4b + c = 0 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} b = - 4a - c \\ a = 4b + c\ \ \ \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} b = - 16b - 4c - c \\ a = 4b + c\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ }\]
\[\left\{ \begin{matrix} 17b = - 5c \\ a = 4b + c \\ \end{matrix} \right.\ \ \]
\[\left\{ \begin{matrix} b = - \frac{5}{17}c \\ a = - \frac{3}{17}c \\ \end{matrix} \right.\ \]
\[\left. \ - \frac{3}{17}cx - \frac{5}{17}cy + c = 0\ \ \ \ \right| \cdot \left( - \frac{17}{c} \right)\]
\[5)\ MK:\ \]
\[\left\{ \begin{matrix} - 2a + 2b + c = 0 \\ - a + 4b + c = 0\ \ \ \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} - 2b - 2c + 2b + c = 0 \\ a = 4b + c\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} - 6b = c\ \ \ \ \\ a = 4b + c \\ \end{matrix} \right.\ \text{\ \ \ }\]
\[\left\{ \begin{matrix} b = - \frac{1}{6}c \\ a = \frac{1}{3}\text{c\ \ \ \ \ } \\ \end{matrix} \right.\ \]
\[\left. \ \frac{1}{3}cx - \frac{1}{6}cy + c = 0\ \ \ \ \right| \cdot \left( \frac{6}{c} \right)\]
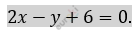
\[\textbf{в)}\ 1)\ l_{1}\bot AB.\ \ \ \]
\[AB:\]
\[3x + 5y - 4 = 0.\]
\[l_{1}:\]
\[ax + by + c = 0.\]
\[5y = 4 - 3x\]
\[y = - \frac{3}{5}x + \frac{4}{5} \Longrightarrow k_{1} = - \frac{3}{5}.\]
\[by = - ax - c\]
\[y = - \frac{a}{b}x - \frac{c}{b} \Longrightarrow k_{2} = - \frac{a}{b}.\]
\[2)\ k_{1} \bullet k_{2} = - 1 \Longrightarrow\]
\[\Longrightarrow - \frac{3}{5} \bullet \left( - \frac{a}{b} \right) = - 1 \Longrightarrow\]
\[\Longrightarrow \frac{3a}{5b} = - 1;\]
\[3a = - 5b \Longrightarrow a = 5;b = - 3 \Longrightarrow\]
\[\Longrightarrow 5x - 3y + c = 0.\]
\[3)\ M \in l_{1}:\ \ \ \]
\[5( - 2) - 3 \bullet 2 + c = 0\]
\[c = 16.\]
\[4)\ l_{2}\bot AC.\ \ \ \]
\[AC:\]
\[x + 6y - 23 = 0.\]
\[l_{2}:\]
\[ax + by + c = 0.\]
\[6y = 23 - x\]
\[y = - \frac{1}{6}x + \frac{23}{6} \Longrightarrow k_{1} = - \frac{1}{6}.\]
\[by = - ax - c\]
\[y = - \frac{a}{b}x - \frac{c}{b} \Longrightarrow k_{2} = - \frac{a}{b}.\]
\[5)\ k_{1} \bullet k_{2} = - 1 \Longrightarrow - \frac{1}{6} \bullet \left( - \frac{a}{b} \right) =\]
\[= - 1 \Longrightarrow \frac{a}{6b} = - 1;\]
\[a = - 6b \Longrightarrow a = 6;b = - 1 \Longrightarrow\]
\[\Longrightarrow 6x - y + c = 0.\]
\[6)\ K \in l_{2}:\ \ \ \]
\[6( - 1) - 4 + c = 0 \Longrightarrow c = 10.\]
\[7)\ l_{3}\bot BC.\ \ \ \]
\[BC:\]
\[2x - y - 7 = 0.\]
\[l_{3}:\]
\[ax + by + c = 0.\]
\[- y = 7 - 2x\]
\[y = 2x - 7 \Longrightarrow k_{1} = 2.\]
\[by = - ax - c\]
\[y = - \frac{a}{b}x - \frac{c}{b} \Longrightarrow k_{2} = - \frac{a}{b}.\]
\[8)\ k_{1} \bullet k_{2} = - 1 \Longrightarrow 2 \bullet \left( - \frac{a}{b} \right) =\]
\[= - 1 \Longrightarrow \frac{2a}{b} = 1;\]
\[b = 2a \Longrightarrow a = 1;b = 2 \Longrightarrow\]
\[\Longrightarrow x + 2y + c = 0.\]
\[9)\ N \in l_{3}:\ \ \ \]
\[4 + 2 + c = 0 \Longrightarrow c = - 6.\]
