Решебник по геометрии 7 класс Атанасян ФГОС Задание 1044

 

\[\boxed{\mathbf{1044.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Решение.\]

\[\textbf{а)}\ \overrightarrow{a}\left\{ \frac{1}{4}; - 1 \right\};\ \overrightarrow{b}\left\{ 2;3 \right\}:\]

\[\overrightarrow{a} \bullet \overrightarrow{b} = \frac{1}{4} \bullet 2 + ( - 1) \bullet 3 = \frac{1}{2} - 3 =\]

\[= - 2,5.\]

\[\textbf{б)}\ \overrightarrow{a}\left\{ - 5;6 \right\};\ \overrightarrow{b}\left\{ 6;5 \right\}:\]

\[\overrightarrow{a} \bullet \overrightarrow{b} = - 5 \bullet 6 + 6 \bullet 5 =\]

\[= - 30 + 30 = 0.\]

\[\textbf{в)}\ \overrightarrow{a}\left\{ 1,5;2 \right\};\ \overrightarrow{b}\left\{ 4; - 0,5 \right\}:\]

\[\overrightarrow{a} \bullet \overrightarrow{b} = 1,5 \bullet 4 + 2 \bullet ( - 0,5) =\]

\[= 6 - 1 = 5.\]

\[\boxed{\mathbf{1044.еуроки - ответы\ на\ пятёрку}}\]

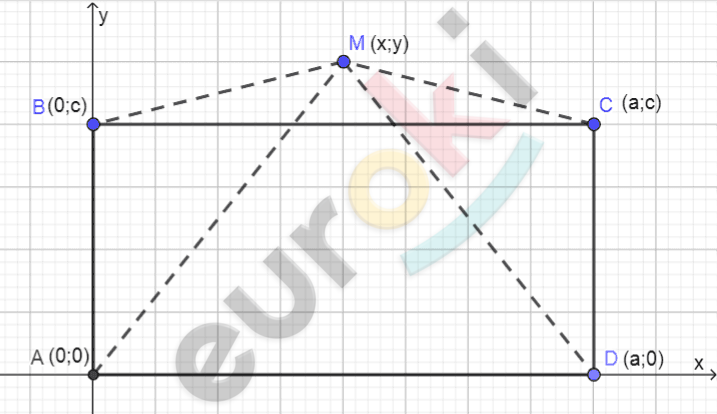
\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[ABCD - прямоугольник.\]

\[\mathbf{Доказать:}\]

\[для\ любой\ точки\ M\]

\[AM^{2} + CM^{2} = BM^{2} + DM^{2}.\]

\[\mathbf{Доказательство.}\]

\[1)\ Введем\ прямоугольную\ \]

\[систему\ координат:\ \]

\[A(0;0);\ D(a;0);B(0;c);C(a;c);\]

\[M(x;y).\]

\[2)\ AM =\]

\[= \sqrt{(x - 0)^{2} + (y - 0)^{2}} =\]

\[= \sqrt{x^{2} + y^{2}}\]

\[AM^{2} = x^{2} + y^{2}.\]

\[CM = \sqrt{(x - a)^{2} + (y - c)^{2}}\]

\[CM^{2} = (x - a)^{2} + (y - c)^{2}.\]

\[BM = \sqrt{(x - 0)^{2} + (y - c)^{2}} =\]

\[= \sqrt{x^{2} + {(y - c)}^{2}}\]

\[BM^{2} = x^{2} + {(y - c)}^{2}.\]

\[DM = \sqrt{(x - a)^{2} + (y - 0)^{2}} =\]

\[= \sqrt{{(x - a)}^{2} + y^{2}}\]

\[DM^{2} = {(x - a)}^{2} + y^{2}.\]

\[3)\ AM^{2} + CM^{2} =\]

\[= x^{2} + y^{2} + (x - a)^{2} + (y - c)^{2};\]

\(BM^{2} + DM^{2} =\)

\[= x^{2} + (y - c)^{2} + (x - a)^{2} + y^{2};\ \]

\[\ AM^{2} + CM^{2} = BM^{2} + DM^{2}.\]

\[Что\ и\ требовалось\ доказать.\]