Решебник по геометрии 7 класс Атанасян ФГОС Задание 103

 

\[\boxed{\mathbf{103}\mathbf{.}\mathbf{ОК}\mathbf{\ }\mathbf{ГДЗ}\mathbf{-}\mathbf{домашка}\mathbf{\ }\mathbf{на}\ 5}\]

\[1)\ Построим\ треугольник\text{\ ABC\ }\]

\[с\ тремя\ острыми\ углами\text{.\ }\]

\[С\ помощью\ чертежного\ \]

\[угольника\ проведем\ в\ нем\ \]

\[высоты\ CE;AF\ и\ \text{BD.}\]

\[2)\ Построим\ треугольник\ \]

\[\text{MNP},\ в\ котором\ угол\ \]

\[M - тупой.\]

\[Проведем\ в\ нем\ высоты\ MS;\]

\[\text{NO\ }и\ \text{PZ.}\]

\[\boxed{\mathbf{103.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунки\ по\ условию\ \mathbf{задачи:}\]

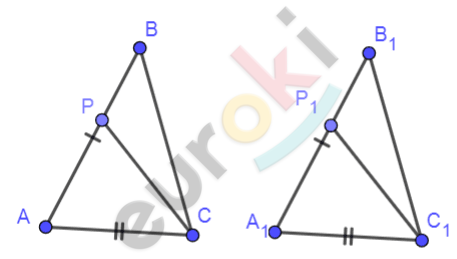
\[\mathbf{Дано:}\]

\[\text{AB} = A_{1}B_{1}\]

\[\text{AC} = A_{1}C_{1}\]

\[\text{AP} = A_{1}P_{1}\]

\[\angle A = \angle A_{1}\]

\[\mathbf{Доказать:}\]

\[BPC = B_{1}P_{1}C_{1}\mathbf{.}\]

\[\mathbf{Доказательство.}\]

\[\mathbf{По\ условию\ задачи:}\]

\[AB = A_{1}B_{1};\ \ \ AC = A_{1}C_{1}.\]

\[По\ первому\ признаку\ \]

\[равенства\ треугольников:\]

\[ABC = A_{1}B_{1}C_{1}.\]

\[Отсюда:\]

\[BC = B_{1}C_{1};\ \ \ \angle B = \angle B_{1};\]

\[BP = AB - AP = A_{1}B_{1} - A_{1}C_{1} =\]

\[= B_{1}P_{1}.\]

\[Следовательно,\ по\ первому\ \]

\[признаку\ равенства\ \]

\[треугольников:\]

\[BPC = P_{1}B_{1}C_{1}.\]

\[\mathbf{Что\ и\ требовалось\ доказать.}\]