Решебник по геометрии 7 класс Атанасян ФГОС Задание 104

 

\[\boxed{\mathbf{104.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Равнобедренные\ \]

\[треугольники\ \text{ABC}.\]

\[\textbf{а)}\ \angle\text{ABC} - острый.\]

\[\textbf{б)}\ \angle\text{ABC} - прямой.\]

\[\textbf{в)}\ \angle\text{ABC} - тупой.\]

\[\boxed{\mathbf{104.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\mathbf{\ задачи:}\]

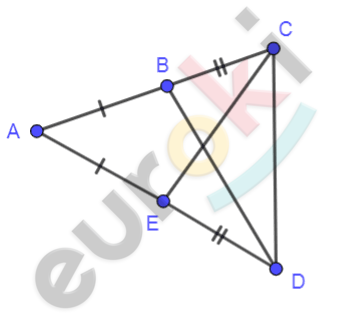
\[\mathbf{Дано:}\]

\[AC = AD\]

\[AB = AE\]

\[\mathbf{Доказать:}\]

\[\angle CBD = \angle DEC.\]

\[\mathbf{Доказательство.}\]

\[\mathbf{По\ условию\ задачи:}\]

\[AC = AD;\ \ \ AE = AB;\ \]

\[\angle A - общий.\]

\[По\ первому\ признаку\ \]

\[равенства\ треугольников:\]

\[ACE = ADB.\]

\[Отсюда:\ \ \ \angle ABD = \angle AEC.\]

\[\angle CBD\ и\ \angle ABD - смежные \Longrightarrow\]

\[\Longrightarrow \angle CBD = 180 - \angle ABD.\]

\[\angle DCE\ и\ \angle AEC - смежные \Longrightarrow\]

\[\Longrightarrow \angle DCE = 180 - \angle AEC.\]

\[Получаем:\]

\[\angle CBD = \angle CED,\ \]

\[так\ как\ \angle ABD = \angle AEC.\]

\[\mathbf{Что\ и\ требовалось\ доказать.}\]