Решебник по геометрии 7 класс Атанасян ФГОС Вопросы для повторения к главе VII

\[\boxed{\mathbf{Вопросы\ для\ повторения\ к\ главе\ }\mathbf{\text{VII}}\mathbf{.еуроки - ответы\ на\ пятёрку}}\]

\[\boxed{\mathbf{1.}}\]

\[\mathbf{Измерение\ }\mathbf{площадей\ }\]

\[\mathbf{проводится\ с\ помощью\ }\]

\[\mathbf{выбранной\ единицы\ }\]

\[\mathbf{изме}\mathbf{рения\ }\mathbf{аналогично\ \ }\]

\[\mathbf{измерению\ длин\ }\mathbf{отрезков.\ }\mathbf{\ }\]

\[\mathbf{За\ единицу\ }\mathbf{измерения\ \ }\]

\[\mathbf{площадей\ }\mathbf{принимают\ \ }\]

\[\mathbf{квадрат,\ сторона\ }\mathbf{которого\ \ }\]

\[\mathbf{равна\ единице\ }\mathbf{измерения\ }\]

\[\mathbf{отрезков}\mathbf{.}\]

\[\mathbf{Обычно\ измеряют\ }\mathbf{лишь\ \ }\]

\[\mathbf{некоторые\ связанные\ }\mathbf{с\ \ }\]

\[\mathbf{многоугольником\ }\mathbf{отрезки,\ }\]

\[\mathbf{а\ затем\ вычисляют\ }\mathbf{п}\mathbf{лощадь\ по\ }\]

\[\mathbf{определённым\ }\mathbf{формулам}\mathbf{.}\]

\[\boxed{\mathbf{2.}}\]

\[Основные\ свойства\ площадей\ \]

\[многоугольников:\]

\[1)\ равные\ многоугольники\ \]

\[имеют\ равные\ площади;\]

\[2)\ если\ многоугольник\ \]

\[составлен\ из\ нескольких\ \]

\[многоугольников,\ то\ его\ \]

\[площадь\ равна\ \ сумме\ \]

\[площадей\ этих\ \]

\[многоугольников;\]

\[3)\ площадь\ квадрата\ равна\ \]

\[квадрату\ его\ стороны.\]

\[\boxed{\mathbf{3.}}\]

\[\mathbf{Если\ площади\ двух\ }\]

\[\mathbf{многоугольников\ равны,\ }\]

\[\mathbf{то\ эти\ }\mathbf{многоугольники\ \ }\]

\[\mathbf{называются\ }\mathbf{равновеликими.}\]

\[\mathbf{Если\ один\ многоугольник\ }\]

\[\mathbf{разрезан\ на\ несколько\ }\]

\[\mathbf{многоугольников\ и\ из\ них\ }\]

\[\mathbf{со}\mathbf{ставлен\ другой\ }\]

\[\mathbf{многоугольник,\ то\ }\mathbf{такие\ }\mathbf{\ }\]

\[\mathbf{многоугольники\ называются\ }\]

\[\mathbf{равносоставленными.}\]

\[\boxed{\mathbf{4.}}\]

\[Теорема:\]

\[площадь\ прямоугольника\ \]

\[равна\ произведению\ его\ \]

\[смежных\ сторон.\]

\[Дано:\]

\[прямоугольник;\]

\[a;b - стороны\ \]

\[прямоугольника.\]

\[Доказать:\]

\[S = \text{ab.}\]

\[Доказательство.\]

\[1)\ Достроим\ прямоугольник\ \]

\[до\ квадрата,\ сторона\ \]

\[которого = (a + b).\]

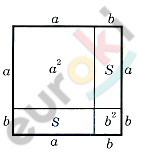
\[2)\ Площадь\ квадрата\ \]

\[(по\ свойству\ 3):\]

\[(a + b)^{2}\text{.\ }\]

\[3)\ С\ другой\ стороны,\ площадь\ \]

\[квадрата\ равна\ сумме\ \]

\[площадей\ составляющих\ \]

\[его\ частей:\]

\[(a + b)^{2} = S + S + a^{2} + b^{2}\]

\[a^{2} + 2ab + b^{2} = 2S + a^{2} + b^{2}\]

\[2S = 2ab\]

\[S = ab.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{5.}}\]

\[\mathbf{Теорема:}\]

\[\mathbf{площадь\ параллелограмма\ }\]

\[\mathbf{равна\ произведению\ его\ }\]

\[\mathbf{основания\ на\ высоту}\mathbf{.}\]

\[\mathbf{Дано:}\]

\[ABCD - параллелограмм;\]

\[h - высота;\]

\[AB = CD = a.\]

\[\mathbf{Доказать}\mathbf{:\ \ }\]

\[S_{\text{ABCD}} = a \cdot h.\]

\[\mathbf{Доказательство.}\]

\[1)\ Если\ он\ не\ является\ \]

\[прямоугольником,\ то\ один\ из\ \]

\[его\ углов\ A\ или\ B\ острый,\ \]

\[пусть\ для\ определенности\ \]

\[угол\ A - острый.\]

\[3)\ Опустим\ перпендикуляр\ \text{AE\ }\]

\[из\ вершины\ \text{A\ }на\ прямую\ CD,\ \]

\[площадь\ трапеции\ \text{ABCE\ }\]

\[равна\ сумме\ площадей\ \]

\[параллелограмма\ \text{ABCD\ }и\]

\[треугольника\ ADE:\]

\[S_{\text{ABCE}} = S_{\text{ABCD}} + S_{\text{ADE}}.\]

\[4)\ Опустим\ перпендикуляр\ \text{BF\ }\]

\[из\ вершины\ \text{B\ }на\ прямую\ CD,\ \]

\[тогда\ площадь\ трапеции\ \text{ABCE\ }\]

\[равна\ сумме\ площадей\ \]

\[прямоугольника\ \text{ABFE}\]

\[и\ треугольника\ BCF:\]

\[S_{\text{ABCE}} = S_{\text{ABFE}} + S_{\text{BCF}}.\]

\[5)\ Так\ как\ отрезки\ \text{AE\ }и\ \text{BF\ }\]

\[равны\ расстоянию\ между\ \]

\[параллельными\ прямыми\ AB\ \]

\[и\ CD,\ то\ они\ являются\ \]

\[высотами\ параллелограмма\ \]

\[\text{ABCD},опущенными\ на\ \]

\[сторону\ AB:\ \ \]

\[AE = BF = h.\]

\[6)\ Рассмотрим\ параллельные\ \]

\[прямые\ \text{AD\ }и\ \text{BC\ }и\ секущую\ DC:\]

\[\angle ADE = \angle BCF\ \]

\[(как\ соответственные\ углы).\]

\[7)\ Тогда\ прямоугольные\ \]

\[треугольники\ \text{ADE\ }и\ \text{BCF\ }\]

\[равны\ по\ катету\ и\]

\[противолежащему\ острому\ \]

\[углу:\]

\[они\ имеют\ равные\ площади;\]

\[S_{\text{ADE}} = S_{\text{BCF}}.\]

\[8)\ Значит,\ площади\ \]

\[параллелограмма\ \text{ABCD\ }и\ \]

\[прямоугольника\ ABFE\ равны:\]

\[S_{\text{ABCD}} = S_{\text{ABFE}} = AB \bullet BF = a \bullet h\mathbf{.}\]

\[\mathbf{Что\ и\ требовалось\ доказать}\mathbf{.}\]

\[\boxed{\mathbf{6.}}\]

\[\mathbf{Теорема:}\]

\[площадь\ треугольника\ равна\ \]

\[половине\ произведения\ его\ \]

\[основания\ на\ высоту.\]

\[Дано:\]

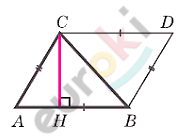
\[⊿ABC;\]

\[AB - основание;\]

\[CH - высота.\]

\[Доказать:\]

\[S = \frac{1}{2}AB \cdot CH.\]

\[\mathbf{Доказательство.}\]

\[1)\ Достроим\ треугольник\ до\ \]

\[параллелепипеда\ \text{ABDC.}\]

\[2)\ ⊿ABC = ⊿DCB - по\ трем\ \]

\[сторонам:\]

\[BC - общая\ сторона;\]

\[AB = CD;\ \ AC = BD - как\ \]

\[противоположные\ стороны\ \]

\[параллелограмма.\]

\[Отсюда:\]

\[площади\ треугольников\ \]

\[равны.\]

\[Следовательно:\]

\[S_{\text{ABC}} = \frac{1}{2}S_{\text{ABCD}} = \frac{1}{2}AB \cdot CH.\]

\[Что\ и\ требовалось\ доказать.\]

\[Площадь\ прямоугольного\ \]

\[треугольника\ равна\ половине\ \]

\[произведения\ его\ катетов.\]

\[\boxed{\mathbf{7.}}\]

\[\mathbf{Теорема:}\]

\[\mathbf{если\ угол\ одного\ }\mathbf{треугольни}\mathbf{ка\ }\]

\[\mathbf{равен\ углу\ другого\ }\]

\[\mathbf{треугольника,\ }\mathbf{то\ площади\ }\]

\[\mathbf{этих\ треугольников\ относятся\ }\]

\[\mathbf{как\ }\mathbf{произведения\ сторон,\ }\]

\[\mathbf{заключающих\ равные}\mathbf{\ углы}\mathbf{.}\]

\[Дано:\]

\[⊿ABC;\]

\[CH - высота;\]

\[S - площадь;\]

\[⊿A_{1}B_{1}C_{1};\]

\[C_{1}H_{1} - высота;\]

\[S_{1} - площадь;\]

\[\angle A = \angle A_{1}.\]

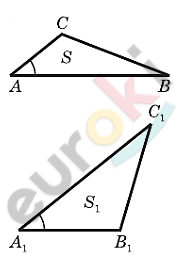
\[Доказать:\]

\[\frac{S}{S_{1}} = \frac{AB \cdot AC}{A_{1}B_{1} \cdot A_{1}C_{1}}.\]

\[Доказательство.\]

\[1)\ Наложим\ ⊿A_{1}B_{1}C_{1}\ на\ ⊿ABC\ \]

\[так,\ чтобы\ вершина\ A_{1}\ \]

\[совместилась\ с\ вершиной\ A,\ \]

\[стороны\ A_{1}B_{1}\ и\ A_{1}C_{1}\ \]

\[наложились\ на\ лучи\ \text{AB\ }и\ \text{AC}.\]

\[2)\ ⊿ABC\ и\ ⊿AB_{1}\text{C\ }имеют\ \]

\[общую\ высоту\ CH:\]

\[\frac{S}{S_{AB_{1}C}} = \frac{\text{AB}}{AB_{1}}.\]

\[3)\ ⊿AB_{1}\text{C\ }и\ ⊿AB_{1}C_{1}\ имеют\ \]

\[общую\ высоту\ B_{1}H_{1}:\]

\[\frac{S_{AB_{1}C}}{S_{AB_{1}C_{1}}} = \frac{\text{AC}}{AC_{1}}.\]

\[4)\ Перемножая\ полученные\ \]

\[равенства,\ получаем:\]

\[\frac{S}{S_{1}} = \frac{AB \cdot AC}{A_{1}B_{1} \cdot A_{1}C_{1}}.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{8.}}\]

\[\mathbf{Теорема:}\]

\[площадь\ трапеции\ равна\ \]

\[произведению\ полусуммы\ \]

\[ее\ оснований\ на\ высоту.\]

\[Дано:\]

\[ABCD - трпаеция;\]

\[AD;BC - основания;\]

\[BH - высота.\]

\[Доказать:\]

\[S = \frac{1}{2}(AD + BC) \cdot BH.\]

\[Доказательство.\]

\[Диагональ\ BD\ делит\ трапецию\ \]

\[на\ два\ треугольника\ \text{ABD\ }и\ \]

\[BCD:\]

\[S = S_{\text{ABD}} + S_{\text{BCD}}.\]

\[В\ треугольнике\ ABD:\]

\[AD - основание;\]

\[BH - высота.\]

\[В\ треугольнике\ BCD:\]

\[\text{BC} - основание;\]

\[DH_{1} - высота.\]

\[Получаем\ (DH_{1} = BH):\]

\[S_{\text{ABD}} = \frac{1}{2}AD \cdot BH;\]

\[S_{\text{BCD}} = \frac{1}{2}BC \cdot DH_{1} = \frac{1}{2}BC \cdot BH.\]

\[Следовательно:\]

\[S = \frac{1}{2}AD \cdot BH + \frac{1}{2}BC \cdot BH =\]

\[= \frac{1}{2}(AD + BC) \cdot BH.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{9.}}\]

\[Теорема\ Пифагора:\]

\[в\ прямоугольном\ \]

\[треугольнике\ квадрат\ \]

\[гипотенузы\ равен\ сумме\]

\[квадратов\ катетов.\]

\[Дано:\]

\[прямоугольный\ треугольник;\]

\[a;b - катеты;\]

\[c - гипотенуза.\]

\[Доказать:\]

\[c^{2} = a^{2} + b^{2}.\]

\[Доказательство.\]

\[1)\ Достроим\ треугольник\ до\ \]

\[квадрата\ со\ стороной\ (a + b).\]

\[2)\ S_{кв} = (a + b)^{2}.\]

\[3)\ Квадрат\ составлен\ из\ \]

\[четырех\ равных\ \]

\[треугольников,\ площадь\]

\[каждого\ равна\ \frac{1}{2}\text{ab\ }и\ квадрата\ \]

\[со\ стороной\ c:\]

\[S = 4 \cdot \frac{1}{2}ab + c^{2} = 2ab + c^{2}.\]

\[4)\ Запишем\ равенство:\]

\[(a + b)^{2} = 2ab + c^{2}\]

\[a^{2} + 2ab + b^{2} = 2ab + c^{2}\]

\[a^{2} + b^{2} = c^{2}.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{10.}}\]

\[Теорема:\]

\[если\ квадрат\ одной\ стороны\ \]

\[треугольника\ равен\ сумме\ \]

\[квадратов\ двух\ других\ сторон,\ \]

\[то\ треугольник\ \]

\[прямоугольный.\]

\[Дано:\]

\[⊿ABC;\]

\[AB^{2} = AC^{2} + BC^{2}.\]

\[Доказать:\]

\[⊿ABC - прямоугольный.\]

\[Доказательство.\]

\[Рассмотрим\ прямоугольный\ \]

\[треугольник\ A_{1}B_{1}C_{1};\ \ \]

\[\angle C_{1} = 90{^\circ}.\]

\[По\ теореме\ Пифагора:\]

\[A_{1}B_{1}^{2} = A_{1}C_{1}^{2} + B_{1}C_{1}^{2}\]

\[A_{1}B_{1}^{2} = AC^{2} + BC^{2}\]

\[A_{1}B_{1}^{2} = AB^{2}\]

\[A_{1}B_{1} = AB.\]

\[⊿ABC = ⊿A_{1}B_{1}C_{1} - по\ трем\ \]

\[сторонам:\]

\[A_{1}C_{1} = AC;\]

\[B_{1}C_{1} = BC;\]

\[A_{1}B_{1} = AB.\]

\[Отсюда:\]

\[\angle C = \angle C_{1} = 90{^\circ};\]

\[⊿ABC - прямоугольный.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{11.}}\]

\[\mathbf{Прямоугольные\ \ треугольники,\ }\]

\[\mathbf{у\ \ которых\ длины\ \ сторон\ \ }\]

\[\mathbf{выражаются\ \ целыми\ \ числами,\ }\]

\[\mathbf{называются\ пифагоровыми\ }\]

\[\mathbf{треугольниками.}\]

\[\mathbf{Примеры:}\]

\[12,\ 5,\ 13;\]

\[3,\ 4,\ 5.\]

\[\boxed{\mathbf{12.}}\]

\[Формула\ Герона:\]

\[S = \sqrt{p(p - a)(p - b)(p - c)};\ \ \]

\[где\ a;b;c - стороны\ \]

\[треугольника;\]

\[p = \frac{a + b + c}{2} - полупериметр\ \]

\[треугольника.\]

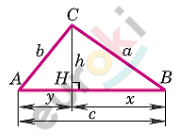
\[Дано:\]

\[⊿ABC;\]

\[AB = c;\]

\[BC = a;\]

\[AC = b.\]

\[Доказать:\ \]

\[S = \sqrt{p(p - a)(p - b)(p - c)}.\]

\[Доказательство.\]

\[Пусть\ \angle A\ и\ \angle B - острые\ углы\ \]

\[треугольника.\]

\[CH\bot AB - высота.\]

\[Пусть\ CH = h;\ \ AH = y;HB = x.\]

\[По\ теореме\ Пифагора:\]

\[a^{2} - x^{2} = h^{2} = b^{2} - y^{2}\]

\[y^{2} - x^{2} = b^{2} - a^{2}\]

\[(y - x)(y + x) = b^{2} - x^{2}.\]

\[Так\ как\ y + x = c:\]

\[y - x = \frac{1}{c}\left( b^{2} - a^{2} \right).\]

\[Сложим\ два\ последних\ \]

\[равенства\ и\ разделим\ их\ на\ 2:\]

\[y = \frac{b^{2} + c^{2} - a^{2}}{2}.\]

\[Отсюда:\]

\[h^{2} = b^{2} - y^{2} =\]

\[= (b + y)(b - y) =\]

\[Следовательно:\]

\[h = \frac{2\sqrt{p(p - a)(p - b)(p - c)}}{c};\]

\[S = \frac{1}{2}\text{hc.}\]

\[Получаем:\]

\[S = \sqrt{p(p - a)(p - b)(p - c)}.\]

\[Что\ и\ требовалось\ доказать.\]