Решебник по геометрии 7 класс Атанасян ФГОС Вопросы для повторения к главе VI

\[\boxed{\mathbf{Вопросы\ для\ повторения\ к\ главе\ }\mathbf{\text{VI}}\mathbf{.еуроки - ответы\ на\ пятёрку}}\]

\[\boxed{\mathbf{1.}}\]

\[\mathbf{Выпуклым\ многоугольником\ }\]

\[\mathbf{называется\ многоугольник,\ }\]

\[\mathbf{обладающий\ тем\ свойством,\ }\]

\[\mathbf{что\ все\ его\ точки\ лежат\ по\ }\]

\[\mathbf{одну\ сторону\ от\ любой}\mathbf{\ }\mathbf{прямой,\ }\]

\[\mathbf{проходящей\ через\ две\ его\ }\]

\[\mathbf{соседние\ вершины}\mathbf{.}\]

\[\mathbf{Углом\ выпуклого\ }\]

\[\mathbf{многоугольника\ при\ заданной\ }\]

\[\mathbf{вершине\ называется\ угол,\ }\]

\[\mathbf{образованный\ его\ сторонами,\ }\]

\[\mathbf{сходящимися\ в\ этой\ вершине.}\]

\[\boxed{\mathbf{2.}}\]

\[\mathbf{Дано:}\]

\[\mathbf{Решение.}\]

\[1)\ Пусть\ A_{1}A_{2}\ldots A_{n} - данный\ \]

\[выпуклый\ многоугольник\ и\ \]

\[n > 3.\]

\[2)\ Проведем\ (n - 3)\ диагонали:\ \ \]

\[A_{1}A_{3},\ A_{1}A_{4},\ \ldots,A_{1}A_{(n - 1)}.\]

\[3)\ Так\ как\ многоугольник\ \]

\[выпуклый,\ то\ эти\ диагонали\ \]

\[разбивают\ его\ на\ (n - 2)\ \]

\[треугольника:\ \ \]

\[\mathrm{\Delta}A_{1}A_{2}A_{3},\ \mathrm{\Delta}A_{1}A_{3}A_{4},\ldots,\ \mathrm{\Delta}A_{1}A_{n - 1}A_{n}.\]

\[4)\ Сумма\ углов\ \]

\[многоугольника\ A_{1}A_{1}\ldots A_{n}\ \]

\[совпадает\ с\ суммой\ углов\ \]

\[всех\ этих\ треугольников.\]

\[5)\ Сумма\ углов\ каждого\ \]

\[треугольника\ равна\ 180{^\circ},\ \]

\[а\ так\ как\ число\ этих\]

\[треугольников\ есть\ (n - 2),\ \]

\[то\ сумма\ углов\ выпуклого\ \]

\[n\text{-}угольника\ A_{1}A_{2}\ldots A_{n}\ равна:\]

\[180{^\circ} \bullet (n - 2).\]

\[Ответ:\ \ 180{^\circ} \bullet (n - 2);\]

\[\boxed{\mathbf{3.}}\]

\[\mathbf{Доказательство.}\]

\[1)\ Внешний\ и\ внутренний\ углы\ \]

\[многоугольника\ являются\ \]

\[смежными.\]

\[Следовательно,\ их\ сумма\ \]

\[равна\ 180{^\circ},\ тогда\ сумма\ всех\ \]

\[внутренних\ и\ внешних\ углов\ \]

\[n\text{-}угольника\ равна:\]

\[S_{1} = n \bullet 180{^\circ}.\]

\[2)\ Сумма\ всех\ внутрениих\ \]

\[углов\ n\text{-}угольника\ равна:\ \ \]

\[S_{2} = 180{^\circ} \bullet (n - 2).\]

\[3)\ Найдем\ сумму\ только\ \]

\[внешних\ углов:\]

\[S = S_{1} - S_{2} =\]

\[= n \bullet 180{^\circ} - 180{^\circ} \bullet (n - 2) =\]

\[= 180n - 180n + 360{^\circ} = 360{^\circ}.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{4.}}\]

\[2)\ Противолежащие\ стороны\ \]

\[этого\ четырехугольника:\ \ \]

\[\text{PQ\ }и\ RS:\ \ PS\ и\ \text{QR.}\]

\[3)\ Противолежащие\ вершины\ \]

\[этого\ четырехугольника:\ \ \]

\[\text{P\ }и\ R;\ \ \ \ \ Q\ и\ \text{S.}\]

\[3)\ Диагонали\ этого\ \]

\[четырехугольника:\]

\[PR;\ \ QS.\]

\[\boxed{\mathbf{5.}}\]

\[\mathbf{Сумма\ углов\ выпуклого\ }\]

\[\mathbf{четырехугольника\ равн}а\ 360{^\circ}.\]

\[\boxed{\mathbf{6.}}\]

\[\mathbf{Параллелограмм\ —\ это\ }\]

\[\mathbf{четырехугольник,\ у\ которого\ }\]

\[\mathbf{противоположные\ стороны\ }\]

\[\mathbf{попарно\ параллельны\ и\ равны.\ \ }\]

\[\mathbf{Параллелограмм\ является\ }\]

\[\mathbf{выпуклым\ }\]

\[\mathbf{четырехугольником.}\]

\[\boxed{\mathbf{7.}}\]

\[\mathbf{Дано:}\]

\[\mathbf{Доказать:\ \ }\]

\[\mathbf{у\ параллелограмма\ }\]

\[\mathbf{противолежащие\ стороны\ }\]

\[\mathbf{равны\ и\ противолежащие\ }\]

\[\mathbf{углы\ равны}\mathbf{.}\]

\[\mathbf{Доказательство.}\]

\[1)\ Пусть\ ABCD - данный\ \]

\[параллелограмм.\]

\[2)\ Проведем\ диагонали\ \]

\[параллелограмма\ и\ отметим\ \]

\[точку\ \text{O\ }на\ их\ пересечении:\]

\[AO = OC\ \ и\ \ BO = OD.\]

\[4)\ ⊿AOB = ⊿COD - по\ первому\ \]

\[признаку.\]

\[\angle AOB = \angle COD;\]

\[\angle AOD = \angle COB\ \]

\[(как\ вертикальные\ углы).\]

\[Отсюда:\]

\[AB = CD.\]

\[5)\ ⊿\text{BOC} = ⊿AOD - по\ первому\ \]

\[признаку,\ отсюда:\]

\[BC = AD.\]

\[6)\ ⊿ABC = ⊿ADC - по\ \]

\[третьему\ признаку,\ отсюда:\]

\[\angle ABC = \angle ADC.\]

\[7)\ ⊿ABD = ⊿CBD - по\ \]

\[третьему\ признаку,\ отсюда:\]

\[\angle BAC = \angle BCD.\]

\[8)\ Таким\ образом,\ у\ \]

\[параллелограмма\ \text{ABCD\ }\]

\[противолежащие\ стороны\]

\[и\ противолежащие\ углы\ \]

\[равны.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{8.}}\]

\[Дано:\]

\[\text{ABCD} - параллелограмм;\]

\[\text{AC};BD - диагонали;\]

\[O - точка\ пересечения\ \]

\[диагоналей.\ \]

\[Доказать:\ \ \]

\[AO = OC;\]

\[DO = OB.\]

\[Доказательство.\]

\[1)\ ABCD - параллелограмм:\]

\[AD \parallel BC.\]

\[2)\ AD \parallel BC;\ \ AC;BD - секущие:\]

\[\angle 1 = \angle 4;\ \ \angle 2 = \angle 3 - как\ \]

\[накрест\ лежащие.\]

\[3)\ ⊿AOD = ⊿BOC - по\ стороне\ \]

\[и\ двум\ прилежащим\ углам.\]

\[AD = BC - как\ \]

\[противоположные\ стороны\ \]

\[параллелограмма;\]

\[\angle 1 = \angle 4;\ \ \angle 2 = \angle 3.\]

\[4)\ Из\ равенства\ треугольников\ \]

\[следует:\]

\[AO = OC;\]

\[DO = OB.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{9.}}\]

\[Если\ в\ четырехугольнике\ две\ \]

\[стороны\ равны\ и\ параллельны,\ \]

\[то\ этот\ четырехугольник -\]

\[параллелограмм.\]

\[Дано:\]

\[ABCD - четырехугольник;\]

\[AD = BC;\]

\[AD \parallel BC.\]

\[Доказать:\]

\[ABCD - параллелограмм.\]

\[Доказательство.\]

\[AD \parallel BC;\ \ AC - секущая:\]

\[\angle 1 = \angle 3.\]

\[⊿ABC = ⊿ADC - по\ первому\ \]

\[признаку:\]

\[AC - общая;\]

\[\angle 1 = \angle 3;\]

\[AD = BC - по\ условию.\]

\[Отсюда:\]

\[\angle 2 = \angle 4.\]

\[Но\ \angle 2\ и\ \angle 4 - накрест\ лежащие\ \]

\[при\ пересечении\ прямых\ \text{AB\ }и\ \]

\[\text{DC}\ и\ секущей\ AC:\]

\[AB \parallel DC.\]

\[Получили:\]

\[AD \parallel BC;\ \ AB \parallel DC:\]

\[в\ четырехугольнике\ \]

\[противоположные\ стороны\ \]

\[попарно\ параллельны;\]

\[ABCD - параллелограмм.\]

\[Что\ и\ требовалось\ доказать.\]

\[Если\ в\ четырехугольнике\ \]

\[противоположные\ стороны\ \]

\[попарно\ параллельны,\ то\ этот\ \]

\[четырехугольник -\]

\[параллелограмм.\]

\[Дано:\]

\[ABCD - четырехугольник;\]

\[AB = DC;\]

\[AD = BC.\]

\[Доказать:\]

\[ABCD - параллелограмм.\]

\[Доказательство.\]

\[Проведем\ диагональ\ \text{AC.}\]

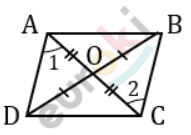
\[⊿ABC = ⊿ADC - по\ третьему\ \]

\[признаку:\]

\[AB = DC;\]

\[AD = BC - по\ условию;\]

\[AC - общая\ сторона.\]

\[Отсюда:\]

\[\angle 1 = \angle 2.\]

\[Но\ \angle 1\ и\ \angle 2\ накрест\ лежащие\ \]

\[при\ пересечении\ прямых\ \text{AD\ }и\ \]

\[\text{BC\ }и\ секущей\ \text{AC}:\]

\[AD \parallel BC - по\ признаку\ \]

\[параллельности\ прямых.\]

\[Получаем:\]

\[AD = BC;\ \ AD \parallel BC.\]

\[Что\ и\ требовалось\ доказать.\]

\[Если\ в\ четырехугольнике\ \]

\[диагонали\ пересекаются\ и\ \]

\[точкой\ пересечения\ делятся\ \]

\[пополам,\ то\ этот\ \]

\[четырехугольник\ \]

\[параллелограмм.\]

\[Дано:\]

\[ABCD - четырехугольник;\]

\[AC;BD - диагонали;\]

\[O - точка\ пересечения\ \]

\[диагоналей;\]

\[AO = OC;\]

\[DO = OB.\]

\[Доказать:\]

\[ABCD - параллелограмм.\]

\[Доказательство.\]

\[⊿AOD = ⊿BOC - по\ первому\ \]

\[признаку:\]

\[AO = OC;\]

\[DO = OB - по\ условию;\]

\[\angle AOD = \angle BOC - как\ \]

\[вертикальные.\]

\[Отсюда:\]

\[AD = BC;\]

\[\angle 1 = \angle 2.\]

\[При\ этом\ \angle 1\ и\ \angle 2 - накрест\]

\[лежащие\ при\ пересечении\ \]

\[прямых\ \text{AD\ }и\ \text{BC\ }и\ секущей\ \text{AC}:\]

\[AD \parallel BC - по\ признаку\ \]

\[параллельности\ двух\ прямых.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{10.}}\]

\[\mathbf{Трапецией\ называется\ }\]

\[\mathbf{четырехугольник,у\ которого\ }\]

\[\mathbf{только\ две}\mathbf{\ }\mathbf{противолежащие\ }\]

\[\mathbf{стороны\ параллельны.}\]

\[\mathbf{Эти\ параллельные\ стороны\ }\]

\[\mathbf{называются\ основаниями\ }\]

\[\mathbf{трапеции.}\]

\[\mathbf{Две\ другие\ называются\ }\]

\[\mathbf{боковыми\ сторонами.}\]

\[\boxed{\mathbf{11.}}\]

\[\mathbf{Трапеция,\ у\ которой\ боковые\ }\]

\[\mathbf{стороны\ равны,\ называется\ }\]

\[\mathbf{равнобедренной\ трапецией\ }\]

\[\left( \mathbf{реже\ равнобокой} \right)\mathbf{\text{.\ }}\]

\[\mathbf{Трапеция,\ имеющая\ прямые\ }\]

\[\mathbf{углы\ при\ боковой\ стороне,\ }\]

\[\mathbf{называется\ прямоугольной}\mathbf{.}\]

\[\boxed{\mathbf{12.}}\]

\[\mathbf{Прямоугольником\ называют\ }\]

\[\mathbf{параллелограмм,\ у\ которого\ }\]

\[\mathbf{все\ углы\ прямые.}\mathbf{\ }\]

\[\mathbf{Прямоугольник\ обладает\ }\]

\[\mathbf{всеми\ свойствами\ }\]

\[\mathbf{параллелограмма.}\]

\[\boxed{\mathbf{13.}}\]

\[\mathbf{Дано:}\]

\[ABCD - прямоугольник;\]

\[AC;BD - диагонали.\]

\[Доказать:\ \ \]

\[AC = BD.\]

\[Доказательство.\]

\[Так\ как\ прямоугольник\ \]

\[является\ параллелограммом,\ \]

\[то\ его\ его\ противолежащие\ \]

\[стороны\ равны:\ \ \]

\[AB = CD;\ \ BC = AD.\]

\[⊿BAD = ⊿CDA -\]

\[прямоугольные;\ \]

\[по\ двум\ катетам:\]

\[BA = CD;\]

\[AD - общий\ катет.\]

\[Отсюда\ следует\ равенство\ \]

\[их\ гипотенуз:\ \]

\[AC = BD.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{14.}}\]

\[Дано:\]

\[ABCD - параллелограмм;\]

\[AC = BD - диагонали.\]

\[Доказать:\ \]

\[ABCD - прямоугольник.\]

\[\mathbf{Доказательство:}\]

\[Противолежащие\ стороны\ и\ \]

\[углы\ у\ параллелограмма\ \]

\[равны:\]

\[\angle C = \angle A;\ \ \ \]

\[\angle B = \angle D;\ \ \]

\[AB = CD;\text{\ \ }\]

\[BC = AD.\]

\[⊿ABC = ⊿BAD - по\ третьему\ \]

\[признаку,\ отсюда:\]

\[\angle A = \angle B.\]

\[Таким\ образом:\ \]

\[\angle A = \angle B = \angle C = \angle D - то\ есть\ \]

\[в\ параллелограмме\ ABCD\ \]

\[все\ углы\ равны.\]

\[Следовательно,\ он\ является\ \]

\[прямоугольником.\ \]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{15.}}\]

\[\mathbf{Ромб - это\ параллелограмм,\ }\]

\[\mathbf{у\ которого\ все\ стороны\ равны.}\]

\[\boxed{\mathbf{16.}}\]

\[Дано:\]

\[ABCD - ромб.\]

\[Доказать:\]

\[AC\bot BD;\]

\[\angle ADO = \angle CDO.\]

\[Доказательство.\]

\[AD = DC - по\ определению\ \]

\[ромба:\]

\[⊿ADC - равнобедренный.\]

\[По\ свойству\ диагоналей\ \]

\[параллелограмма:\]

\[AO = OC.\]

\[DO - медиана;\ \]

\[⊿ADC - равнобедренный:\]

\[DO - высота\ и\ биссектриса\ \]

\[(по\ свойству\ равнобедренного\ \]

\[треугольника).\]

\[Следовательно:\]

\[AC\bot BD;\]

\[\angle ADO = \angle CDO.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{17.}}\]

\[Квадратом\ называется\ \]

\[прямоугольник,\ у\ которого\ все\ \]

\[стороны\ равны.\]

\[Основные\ свойства\ квадрата:\]

\[1)\ все\ стороны\ равны;\]

\[2)\ все\ углы\ равны\ и\ \]

\[составляют\ 90{^\circ};\]

\[3)\ диагонали\ равны\ и\ \]

\[перпендикулярны;\]

\[4)\ центры\ вписанной\ и\ \]

\[описанной\ окружности\ \]

\[совпадают\ и\ находятся\ \]

\[в\ точке\ пересечения\ \]

\[диагоналей.\]

\[\boxed{\mathbf{18.}}\]

\[Если\ в\ прямоугольнике\ две\ его\ \]

\[смежные\ стороны\ равны,\ то\ он\]

\[является\ квадратом.\]

\[Дано:\]

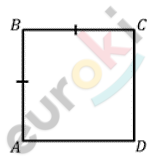
\[ABCD - прямоугольник;\]

\[AB = BC.\]

\[Доказать:\]

\[ABCD - квадрат.\]

\[Доказательство.\]

\[ABCD - прямоугольник:\]

\[его\ противолежащие\ стороны\ \]

\[равны;\]

\[AB = BC;\]

\[CD = AB.\]

\[AB = BC = CD = AD.\]

\[Следовательно:\]

\[ABCD - квадрат\ \]

\[(по\ определению).\]

\[Что\ и\ требовалось\ доказать.\]

\[Если\ в\ прямоугольнике\ \]

\[диагонали\ перпендикулярны,\ \]

\[то\ этот\ прямоугольник -\]

\[квадрат.\]

\[Дано:\]

\[ABCD - прямоугольник;\]

\[AC\bot BD.\]

\[Доказать:\]

\[ABCD - квадрат.\]

\[Доказательство.\]

\[В\ треугольнике\ ABC:\]

\[AO = OC - по\ свойству\ \]

\[диагоналей\ прямоугольника;\]

\[BO - медиана\ \]

\[(по\ определению);\]

\[BO - высота\ (AC\bot BD).\]

\[⊿ABC - равнобедренный\ \]

\[с\ основанием\ AC:\]

\[по\ признаку\ равнобедренного\ \]

\[треугольника.\]

\[Отсюда:\]

\[AB = BC.\]

\[Следовательно:\]

\[ABCD - квадрат\ \]

\[(по\ первому\ признаку\ квадрата).\]

\[Что\ и\ требовалось\ доказать.\]

\[Если\ в\ прямоугольнике\ одна\ из\ \]

\[диагоналей\ является\ \]

\[биссектрисой\ его\ угла,\ то\ такой\ \]

\[прямоугольник - квадрат.\]

\[Дано:\]

\[ABCD - квадрат;\]

\[BD - диагональ;\]

\[BD - биссектриса\ \angle B.\]

\[Доказать:\]

\[ABCD - квадрат.\]

\[Доказательство.\]

\[BD - биссектриса\ \angle B:\]

\[\angle ABD = \angle DBC.\]

\[По\ свойству\ внутренних\ \]

\[накрест\ лежащих\ углов\ \]

\[при\ параллельных\ прямых:\]

\[\angle ADB = \angle ABD.\]

\[⊿BAD - равнобедренный:\]

\[AB = AD.\]

\[Следовательно:\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{19.}}\]

\[\mathbf{Если\ диагонали\ }\]

\[\mathbf{параллелограмма\ }\]

\[\mathbf{перпендикулярны,\ то\ этот}\]

\[\mathbf{параллелограмм - ромб.\ }\]

\[Дано:\]

\[ABCD - параллелограмм;\]

\[AC\bot BD.\]

\[Доказать:\ \ \]

\[ABCD - ромб.\]

\[Доказательство.\]

\[Диагонали\ \text{AC\ }и\ BD\ \]

\[перепендикулярны\ и\ \]

\[пересекаются\ в\ точке\ \text{O.}\]

\[По\ свойству\ параллелограмма:\ \ \]

\[AO = OC;\text{\ \ }BO = OD.\]

\[2)\ ⊿AOB = ⊿BOC = ⊿COD =\]

\[= ⊿DOA - по\ двум\ катетам,\ \]

\[прямоугольные.\]

\[Отсюда\ следует\ равенство\ \]

\[их\ гипотенуз:\ \ \]

\[AB = BC = CD = DA.\]

\[3)\ Так\ как\ у\ параллелограмма\ \]

\[\text{ABCD\ }все\ стороны\ равны:\]

\[ABCD - ромб\ \]

\[(по\ определению).\]

\[Что\ и\ требовалось\ доказать.\]

\[\mathbf{Если\ диагональ\ }\]

\[\mathbf{параллелограмма\ является\ }\]

\[\mathbf{биссектрисой\ его\ угла,}\]

\[\mathbf{то\ этот\ параллелограмм -}\]

\[\mathbf{ромб.}\]

\[\mathbf{Дано}\mathbf{:}\]

\[ABCD - параллелограмм;\]

\[AC - диагональ\ и\ биссектриса.\]

\[Доказать:\ \]

\[ABCD - ромб.\]

\[Доказательство:\]

\[Диагональ\ AC\ является\ \]

\[биссектрисой\ углов\ A\ и\ C:\]

\[\angle BAC = \angle CAD = \angle BCA =\]

\[= \angle ACD\ (так\ как\ \]

\[противолежащие\ углы\ \]

\[параллелограмма\ равны).\]

\[2)\ ⊿\text{ABC\ }и\ ⊿\text{CDA} -\]

\[равнобедренные;\ \ \]

\[с\ основанием\ AC:\]

\[так\ как\ углы\ при\ AC\ равны.\]

\[3)\ ⊿ABC = ⊿CDA - по\ второму\ \]

\[признаку.\]

\[Отсюда\ следует\ равенство\ их\ \]

\[боковых\ сторон:\ \ \]

\[AB = BC = CD = DA.\]

\[3)\ У\ параллелограмма\ \text{ABCD\ }\]

\[все\ стороны\ равны:\]

\[ABCD - ромб\ \]

\[(по\ определению).\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{20.}}\]

\[\mathbf{Две\ точки\ называются\ }\]

\[\mathbf{симметричными\ относительно\ }\]

\[\mathbf{данной\ точки,\ если\ они\ лежат\ }\]

\[\mathbf{на\ одной\ прямой\ и\ на\ }\]

\[\mathbf{одинаковом\ расстоянии\ }\]

\[\mathbf{от\ данной}\mathbf{\ }\mathbf{точки}\mathbf{.}\]

\[\boxed{\mathbf{21.}}\]

\[\mathbf{Фигура\ называется\ }\]

\[\mathbf{симметричной\ относительно\ }\]

\[\mathbf{точки\ ,\ если\ для\ любой\ точки\ }\]

\[\mathbf{фигуры\ точка,\ симметричная\ }\]

\[\mathbf{ей,\ также\ принадлежит\ данной}\mathbf{\ }\]

\[\mathbf{фигуре.\ }\]

\[\mathbf{Точка\ \ называется\ центром\ }\]

\[\mathbf{симметрии,\ а\ фигура\ обладает\ }\]

\[\mathbf{центральной\ симметрией}\mathbf{.}\]

\[\boxed{\mathbf{22.}}\]