Решебник по геометрии 7 класс Атанасян ФГОС Вопросы для повторения к главе V

\[\boxed{\mathbf{Вопросы\ для\ повторения\ к\ главе\ }\mathbf{V}\mathbf{.еуроки - ответы\ на\ пятёрку}}\]

\[\boxed{\mathbf{1.}}\]

\[Геометрическое\ место\ точек\ \]

\[(ГМТ)—\ это\ фигура,\ состоящая\ \]

\[из\ всех\ точек\ плоскости,\]

\[удовлетворяющих\ \]

\[определённому\ условию.\]

\[Примеры.\]

\[1)\ Геометрическим\ местом\ \]

\[точек,\ равноудалённых\ от\ двух\ \]

\[данных\ точек,\ является\ \]

\[серединный\ перпендикуляр\ к\ \]

\[отрезку,\ соединяющему\ \]

\[эти\ точки.\]

\[2)\ Геометрическим\ местом\ \]

\[точек,\ равноудалённых\ от\ \]

\[сторон\ \]

\[неразвёрнутого\ угла,\ является\ \]

\[биссектриса\ этого\ угла.\]

\[3)\ Геометрическим\ местом\ \]

\[точек,\ удалённых\ от\ данной\ \]

\[прямой\ на\ расстояние\ h,\ \]

\[состоит\ из\ двух\ прямых,\ \]

\[параллельных\ данной\ прямой\ \]

\[и\ отстоящих\ от\ неё\ на\ h.\]

\[4)\ Геометрическим\ местом\ \]

\[точек,\ равноудалённых\ от\ \]

\[двух\ параллельных\ прямых,\ \]

\[является\ прямая,\ параллельная\ \]

\[этим\ прямым\ и\ проходящая\ \]

\[через\ середину\ их\ общего\ \]

\[перпендикуляра.\]

\[\boxed{\mathbf{2.}}\]

\[Теорема:\]

\[биссектриса\ угла\ треугольника\ \]

\[делит\ его\ противоположную\ \]

\[сторону\ в\ пропорции,\ равной\ \]

\[отношению\ прилежащих\ к\ \]

\[данному\ углу\ сторон.\]

\[Дано:\]

\[⊿ABC;\]

\[AD - биссектриса\ \angle A.\]

\[Доказать:\]

\[\frac{\text{BD}}{\text{CD}} = \frac{\text{AB}}{\text{AC}}.\]

\[Доказательство.\]

\[Построим\ высоту\ AH\ \]

\[треугольника.\]

\[Найдем\ площади\ \]

\[треугольников\ ABD;ACD:\]

\[S_{\text{ABD}} = \frac{1}{2}AH \cdot BD;\]

\[S_{\text{ACD}} = \frac{1}{2}AH \cdot CD.\]

\[Получим\ соотношение:\]

\[\frac{S_{\text{ABD}}}{S_{\text{ACD}}} = \frac{\frac{1}{2}AH \cdot BD}{\frac{1}{2}AH \cdot CD} = \frac{\text{BD}}{\text{CD}}.\]

\[Площади\ треугольников\ \]

\[можно\ найти\ другим\ способом:\]

\[S_{\text{ABD}} = \frac{1}{2}AB \cdot AD \cdot \sin\alpha;\]

\[S_{\text{ACD}} = \frac{1}{2}AD \cdot AC \cdot \sin\alpha.\]

\[Тогда\ соотношение:\]

\[\frac{S_{\text{ABD}}}{S_{\text{ACD}}} = \frac{\frac{1}{2}AB \cdot AD \cdot \sin\alpha}{\frac{1}{2}AD \cdot AC \cdot \sin\alpha} = \frac{\text{AB}}{\text{AC}}.\]

\[Следовательно:\]

\[\frac{\text{BD}}{\text{CD}} = \frac{\text{AB}}{\text{AC}}.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{3.}}\]

\[\mathbf{Дано:}\]

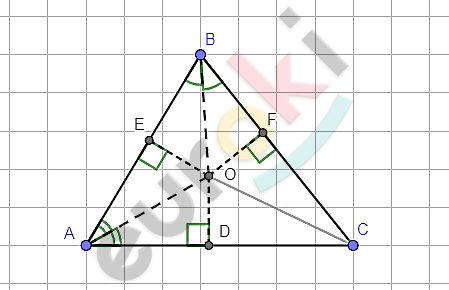
\[\mathbf{Доказать:\ \ }\]

\[\mathbf{все\ три\ биссектрисы\ }\]

\[\mathbf{треугольника\ пересекаются}\]

\[\mathbf{\ в\ одной\ точке.}\]

\[\mathbf{Доказател}\mathbf{ьство}\mathbf{.}\]

\[1)\ Проведем\ биссектрисы\ из\ \]

\[углов\ A\ и\ B\ произвольного\ \]

\[треугольника\ ABC,\ они\ \]

\[пересекутся\ в\ некоторой\ \]

\[точке\ \text{O.}\]

\[2)\ Опустим\ из\ точки\ \text{O\ }\]

\[перпендикуляры\ OD,\ OE\ и\ \text{OF\ }\]

\[на\ стороны\ \mathrm{\Delta}ABC\ как\ показано\ \]

\[на\ рисунке.\]

\[3)\ Прямоугольные\ \]

\[треугольники\ \text{AOD\ }и\ \text{AOE\ }\]

\[равны\ по\ гипотенузе\ и\]

\[острому\ углу\ (AO - общая\ \]

\[гипотенуза\ и\ \angle OAD = \angle OAE\ \]

\[так\ как\ AO - биссектриса\ \]

\[\angle OAE.\]

\[4)\ Из\ равенства\ треугольников\ \]

\[следует\ равенство\ их\ \]

\[катетов\ \text{OD\ }и\ \text{OE.}\]

\[5)\ Аналогично,\ равенство\ \]

\[катетов\ \text{OE\ }и\ \text{OF\ }из\ равенства\ \]

\[треугольников\ BOE\ и\ BOF,\ \]

\[значит,\ катеты\ OD,\ OF\ и\ \text{OE\ }\]

\[равны\ между\ собой.\]

\[6)\ Прямоугольные\ \]

\[треугольники\ COD\ и\ \text{COF\ }\]

\[равны\ по\ гипотенузе\ иькатету\ \]

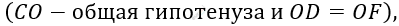
\[отсюда:\ \ \angle OCD = \angle OCF.\]

\[7)\ Следовательно,\ луч\ CO -\]

\[биссектриса\ угла\ \text{C\ }\]

\[треуголььника\ \text{ABC.}\]

\[8)\ Таким\ образом,\ все\ \]

\[биссектрисы\ \mathrm{\Delta}\text{ABC\ }\]

\[пересекаются\ в\ одной\ точке.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{4.}}\]

\[\mathbf{Серединный\ перпендикуляр\ }\]

\[\mathbf{к\ отрезку\ —\ это\ прямая,\ }\]

\[\mathbf{перпендикулярная\ данному\ }\]

\[\mathbf{отрезку\ и\ проходящая\ через\ }\]

\[\mathbf{его\ середину.}\]

\[\boxed{\mathbf{5.}}\]

\[Теорема:\]

\[каждая\ точка\ серединного\ \]

\[перпендикуляра\ к\ отрезку\ \]

\[равноудалена\ от\ концов\ этого\ \]

\[отрезка.\]

\[Дано:\ \]

\[a\bot AB;\]

\[O - точка\ пересечения\ \text{a\ }и\ AB;\]

\[AO = OB;\]

\[M \in a.\]

\[Доказать:\]

\[AM = MB.\]

\[Доказательство.\]

\[1)\ Если\ точка\ M\ совпадает\ \]

\[с\ точкой\ O:\]

\[AM = MB - так\ как\ AO = OB.\]

\[2)\ Если\ M\ и\ O - различные\ \]

\[точки.\]

\[⊿OAM = ⊿OMB - по\ двум\ \]

\[катетам\ \]

\[(a\bot AB;прямоугольные):\]

\[AO = OB - по\ условию;\]

\[OM - общая\ сторона.\]

\[3)\ В\ равных\ треугольниках\ \]

\[соответствующие\ стороны\ \]

\[равны:\]

\[AM = MB.\]

\[Следовательно:\]

\[каждая\ точка\ серединного\ \]

\[перпендикуляра\ к\ отрезку\ \]

\[равноудалена\ от\ концов\ этого\ \]

\[отрезка.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{6.}}\]

\[Дано:\]

\[⊿ABC;\]

\[m;n;k - серединные\ \]

\[перпендикуляры.\]

\[Доказательство.\]

\[Сначала\ докажем,\ что\ \]

\[серединные\ перпендикуляры\ \]

\(к\ двум\ сторонам\) \(треугольника\ \)

\[пересекаются\ в\ одной\ точке.\]

\[Предположим,\ что\ m\ и\ \text{k\ }не\ \]

\[пересекаются;\ \ m \parallel k.\]

\[AC\bot k;\ \ \ k \parallel m:\]

\[AC\bot m.\]

\[AC\bot m;\ \ AB\bot m:\]

\[AC \parallel AB.\]

\[Но\ прямые\ AB\ и\ \text{AC\ }\]

\[пересекаются\ в\ точке\ A:\]

\[пришли\ к\ противоречию.\]

\[Следовательно,\ прямые\ \text{m\ }и\ \]

\[k - пересекаются.\]

\[По\ свойству\ серединного\ \]

\[перпендикуляра\ к\ отрезку\ \]

\[AO = OC;\ AO = BO.\ \]

\[Следовательно,\ и\ OC = BO.\ \]

\[Значит,\ точка\ O\ равноудалена\ \]

\[от\ концов\ отрезка\ BC.\]

\[Следовательно,\ лежит\ на\ \]

\[серединном\ перпендикуляре\ n\ \]

\[к\ этому\ отрезку.\ \]

\[Таким\ образом,\ все\ три\ \]

\[серединных\ перпендикуляра\ \]

\[m,\ n,\ k\ к\ сторонам\ \]

\[треугольника\ ABC\ \]

\[пересекаются\ в\ одной\ точке\ O.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{7.}}\]

\[Окружность\ с\ центром\ О\ и\ \]

\[радиусом\ R\ –\ это\ фигура,\ \]

\[которая\ состоит\ из\ всех\ точек\ \]

\[плоскости\ равноудалённых\ от\ \]

\[точки\ О\ (центр\ окружности)\]

\[на\ расстояние\ R.\]

\[Хорда\ окружности\ —\ отрезок,\ \]

\[соединяющий\ две\ любые\ её\ \]

\[точки.\]

\[Диаметр\ окружности\ —\ это\ \]

\[хорда,\ которая\ проходит\ через\ \]

\[центр\ окружности.\]

\[\boxed{\mathbf{8.}}\]

\[\mathbf{Диаметр\ окружности,\ }\]

\[\mathbf{перпендикулярный\ хорже,\ }\]

\[\mathbf{делит\ эту\ хорду\ пополам.}\]

\[\mathbf{Дано:}\]

\[окружность\ (O;r);\]

\[CD - диаметр;\]

\[AB - хорда.\]

\[Доказать:\]

\[M - середина\ \text{AB.}\]

\[Доказательство.\]

\[1)\ Проведем\ радиусы\ OA\ и\ \text{OB.}\]

\[2)\ Треугольник\ AOB -\]

\[равнобедренный:\]

\[AO = OB = r.\]

\[3)\ В\ равнобедренном\ \]

\[треугольнике\ высота\ является\ \]

\[медианой:\]

\[OM - медиана.\]

\[4)\ Следовательно:\]

\[AM = MB;\]

\[M - середина\ хорды\ \text{AB.}\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{9.}}\]

\[\mathbf{Из\ этого\ следует,\ например,\ }\]

\[\mathbf{что\ если\ центр\ описанной\ }\]

\[\mathbf{окружности\ лежит\ на\ стороне\ }\]

\[\mathbf{треугольника,\ то\ угол\ }\]

\[\mathbf{напротив\ этой\ стороны\ —\ }\]

\[\mathbf{прямой.}\]

\[\mathbf{Если\ центр\ описанной\ }\]

\[\mathbf{окружности\ лежит\ на\ }\]

\[\mathbf{диагонали\ четырехугольника,\ }\]

\[\mathbf{то\ угол\ напротив\ этой\ }\]

\[\mathbf{диагонали\ —\ прямой.}\]

\[\boxed{\mathbf{10.}}\]

\[1)\ Пусть\ даны\ окружность\ \]

\[с\ центром\ в\ точке\ \text{O\ }и\ прямая\ \]

\[AC\ пересекает\ окружность\ в\ \]

\[точках\ A,\ B\ и\ \text{C.}\]

\[2)\ Отрезки\ AO,\ OB\ и\ \text{OC\ }равны\ \]

\[так\ как\ являются\ радиусами.\]

\[3)\ Таким\ образом,\ \]

\[треугольники\ \text{AOB\ }и\ \text{BOC\ }\]

\[равнобедренные\ с\ основанием\ \]

\[\text{AB\ }и\ AC,\ что,\ как\ мы\ знаем,\ \]

\[невозможно.\]

\[Следовательно:\]

\[прямая\ и\ окружность\ не\ могут\ \]

\[пересекаться\ более\ чем\ в\ двух\ \]

\[точках.\]

\[Ответ:\ \ не\ могут.\]

\[\boxed{\mathbf{11.}}\]

\[\mathbf{Секущая\ к\ окружности\ —\ это\ }\]

\[\mathbf{прямая,\ которая\ пересекает\ ее\ }\]

\[\mathbf{в\ двух\ местах,то\ есть\ имеет\ }\]

\[\mathbf{с\ ней\ две\ общие\ точки.}\]

\[\boxed{\mathbf{12.}}\]

\[\mathbf{Прямая,\ имеющая\ с\ }\]

\[\mathbf{окружностью\ только\ одну\ }\]

\[\mathbf{общую\ точку\ называется\ }\]

\[\mathbf{касательной\ к\ окружности.}\]

\[\mathbf{Общая\ точка\ прямой\ и\ }\]

\[\mathbf{окружности\ называется\ }\]

\[\mathbf{точкой\ касания.}\]

\[\boxed{\mathbf{13.}}\]

\[\mathbf{Теорема:}\]

\[касательная\ к\ окружности\ \]

\[перпендикулярна\ к\ радиусу,\ \]

\[проведенному\ в\ точку\ касания.\]

\[Дано:\]

\[окружность\ (O;R);\]

\[R = OA;\]

\[a - касательная;\]

\[A - точка\ касания.\]

\[Доказать:\]

\[a\bot OA.\]

\[Доказательство.\]

\[Доказательство\ от\ противного.\]

\[Предположим,\ что\ радиус\ и\ \]

\[прямая\ \text{a\ }не\ перпендикулярны.\]

\[Опустим\ из\ точки\ \text{O\ }на\ \]

\[прямую\ \text{a\ }перпендикуляр\ \text{OB.}\]

\[OA - наклонная,\ проведенная\ \]

\[из\ точки\ \text{O\ }на\ прямую\ \text{a.}\]

\[По\ свойству\ перпендикуляра\ и\ \]

\[наклонной,\ любая\ наклонная\ \]

\[больше\ перпендикуляра:\]

\[OA > OB.\]

\[Получается,\ расстояние\ от\ \]

\[точки\ O\ до\ прямой\ a\ —\ длина\ \]

\[перпендикуляра\ OB\ —\ меньше\ \]

\[радиуса.\ \]

\[Из\ этого\ следует,\ что\ прямая\ a\ \]

\[и\ окружность\ имеют\ две\ общие\ \]

\[точки.\]

\[Противоречие\ получили,\ так\ \]

\[как\ предположили,\ что\ \]

\[радиус\ OA\ и\ касательная\ a\ \]

\[не\ перпендикулярны.\ \]

\[Значит,\ касательная\ \]

\[перпендикулярна\ к\ радиусу,\ \]

\[проведенному\ в\ точку\ касания:\]

\[a\bot OA.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{14.}}\]

\[\mathbf{Отрезки\ касательных\ }\]

\[\mathbf{к\ окружности,\ проведенные\ из\ }\]

\[\mathbf{одной\ точки,\ равны\ и\ }\]

\[\mathbf{составляют\ равные\ углы\ }\]

\[\mathbf{с\ прямой,\ проходящей\ через\ }\]

\[\mathbf{эту\ точку.}\]

\[\boxed{\mathbf{15.}}\]

\[\mathbf{Обратная\ теорема:}\]

\[\mathbf{если\ прямая\ проходит\ через\ }\]

\[\mathbf{конец\ радиуса,\ лежащий\ на\ }\]

\[\mathbf{окружности,\ и\ }\]

\[\mathbf{перпендикулярна\ к\ этому\ }\]

\[\mathbf{радиусу,\ то\ она\ является\ }\]

\[\mathbf{касательной.}\]

\[Дано:\]

\[окружность\ (O;r);\]

\[OA = r;\]

\[p - прямая,\ проходящая\ \]

\[через\ точку\ A;\]

\[p\bot OA.\]

\[Доказать:\]

\[p - касательная.\]

\[Доказательство.\]

\[Расстояние\ от\ центра\ \]

\[окружности\ до\ прямой\ равно\ \]

\[длине\ перпендикуляра,\ а\ это\ \]

\[радиус\ окружности\ OA.\ \]

\[Следовательно,\ прямая\ и\ \]

\[окружность\ имеют\ только\ \]

\[одну\ общую\ точку.\ \]

\[Это\ и\ означает,\ что\ прямая\ p\ \]

\[является\ касательной\ к\ \]

\[окружности.\ \]

\[Теорема\ доказана.\]

\[\boxed{\mathbf{16.}}\]

\[\mathbf{Отметить\ на\ окружности\ }\]

\[\mathbf{нужную\ точку.}\]

\[\mathbf{Провести\ отрезок\ из\ центра\ }\]

\[\mathbf{окружности\ к\ данной\ точке.}\]

\[\mathbf{Проводим\ прямую,\ }\]

\[\mathbf{перпендикулярную\ данному\ }\]

\[\mathbf{отрезку\ }\left( \mathbf{радиусу} \right)\mathbf{.}\]

\[\mathbf{Она\ и\ будет\ искомой\ }\]

\[\mathbf{касательной\ к\ окружности.}\]

\[\boxed{\mathbf{17.}}\]

\[\mathbf{Если\ отрезок\ }\left( \mathbf{луч} \right)\]

\[\mathbf{принадлежит\ прямой,\ }\]

\[\mathbf{касательной\ к\ окружности,\ \ }\]

\[\mathbf{и\ точка\ касания\ является\ }\]

\[\mathbf{точкой\ отрезка\ }\left( \mathbf{луча} \right)\mathbf{,\ }\]

\[\mathbf{то\ говорят,\ что\ данный\ отрезок\ \ }\]

\[\left( \mathbf{луч} \right)\mathbf{является\ касательным\ }\]

\[\mathbf{к\ окружности.\ }\]

\[\boxed{\mathbf{18.}}\]

\[\mathbf{Окружность\ называется\ }\]

\[\mathbf{вписанной\ в\ угол,\ если\ она\ }\]

\[\mathbf{касается\ сторон\ угла.}\]

\[\mathbf{В\ угол\ можно\ вписать\ }\]

\[\mathbf{бесконечно\ много\ }\]

\[\mathbf{окружностей;}\]

\[\mathbf{их\ центры\ будут\ находиться\ }\]

\[\mathbf{на\ биссектрисе\ угла.}\]

\[\boxed{\mathbf{19.}}\]

\[\mathbf{Вписанная\ в\ треугольник\ }\]

\[\mathbf{окружность\ —\ окружность\ }\]

\[\mathbf{внутри\ треугольника,\ }\]

\[\mathbf{касающаяся\ всех\ его\ сторон;\ }\]

\[\mathbf{наибольшая\ окружность,\ }\]

\[\mathbf{которая\ может\ находиться\ }\]

\[\mathbf{внутри\ треугольника.\ }\]

\[\mathbf{Описанным\ около\ окружности\ }\]

\[\mathbf{треугольником\ называют\ }\]

\[\mathbf{такой\ треугольник,\ все\ три\ }\]

\[\mathbf{стороны\ которого\ являются\ }\]

\[\mathbf{касательными\ к\ данной\ }\]

\[\mathbf{окружности\ (другими\ словами,\ }\]

\[\mathbf{все\ стороны\ которого\ }\]

\[\mathbf{касаются\ окружности,\ то\ есть\ }\]

\[\mathbf{имеют\ с\ ней\ одну\ общую\ }\]

\[\mathbf{точку).\ }\]

\[\boxed{\mathbf{20.}}\]

\[\mathbf{Теорема:}\]

\[\mathbf{в\ любой\ треугольник\ можно\ }\]

\[\mathbf{вписать\ окружность,\ причем\ }\]

\[\mathbf{только\ одну.}\]

\[\mathbf{Дано::}\]

\[\mathbf{Доказать:\ \ }\]

\[\mathbf{в\ любой\ треугольник\ можно\ }\]

\[\mathbf{вписать\ окружность.}\]

\[\mathbf{Доказательство.}\]

\[1)\ Пусть\ ABC - данный\ \]

\[треугольник.\]

\[2)\ Проведем\ биссектрисы\ \]

\[углов\ \text{A\ }и\ \text{B\ }они\ пересекутся\ \]

\[в\ некоторой\ точке\ O,\ \]

\[тогда\ \ \angle CAO = \angle OAB\ \ и\ \ \]

\[\angle CBO = \angle OBA.\]

\[3)\ Из\ точки\ \text{O\ }опустим\ \]

\[перпендикуляры\ OA_{1},\ OB_{1}\ и\ \]

\[OC_{1}\ на\ стороны\]

\[треугольника\ \text{ABC.}\]

\[4)\ Прямоугольные\ \]

\[треугольники\ \text{AO}B_{1}\ и\ \text{AO}C_{1}\ \]

\[равны\ по\ гипотенузе\]

\[и\ острому\ углу\ \]

\[(AO - общая\ гипотенуза),\ \]

\[отсюда:\ \ OB_{1} = OC_{1}.\]

\[5)\ Прямоугольные\ \]

\[треугольники\ \text{BO}A_{1}\ и\ \text{BO}C_{1}\ \]

\[равны\ по\ гипотенузе\ и\ острому\ \]

\[углу\ (BO - общая\ гипотенуза),\ \]

\[отсюда:\ \ OC_{1} = OA_{1}.\]

\[6)\ Таким\ образом,\ точки\ A_{1},\ B_{1}\ \]

\[и\ C_{1}\ равноудалены\ от\ точки\ \text{O.\ }\]

\[Значит,они\ принадлежат\ \]

\[одной\ окружности,\ а\ стороны\ \]

\[треугольника\ ABC\ являются\ \]

\[касательными\ к\ этой\ \]

\[окружности,\ то\ есть\ \]

\[в\ треугольник\ ABC\ можно\ \]

\[вписать\ окружность.\]

\[7)\ Прямоугольные\ \]

\[треугольники\ \text{CO}B_{1}\ и\ \text{CO}A_{1}\ \]

\[равны\ по\ катету\ и\ гипотенузе\ \]

\[(CO - общая\ гипотенуза),\ \]

\[отсюда:\ \angle B_{1}CO = \angle A_{1}\text{CO.}\]

\[То\ есть:\]

\[точка\ \text{O\ }лежит\ на\ биссектрисе\ \]

\[угла\ \text{C.}\]

\[8)\ Таким\ образом,\ все\ \]

\[биссектрисы\ треугольника\ \]

\[пересекаются\ в\ одной\ точке.\]

\[Что\ и\ требовалось\ доказать.\]

\[Так\ как\ центр\ вписанной\ \]

\[окружности\ является\ точкой\ \]

\[пересечения\ биссектрис\ \]

\[треугольника,\ то\ он\ может\ \]

\[быть\ только\ один.\]

\[\boxed{\mathbf{21.}}\]

\[\mathbf{Окружность\ называют\ }\]

\[\mathbf{описанной\ около\ }\]

\[\mathbf{треугольника,\ если\ все\ }\]

\[\mathbf{вершины\ треугольника\ }\]

\[\mathbf{расположены\ на\ окружности.\ }\]

\[\mathbf{Её\ центр\ равноудалён\ от\ всех\ }\]

\[\mathbf{вершин,\ то\ есть\ должен\ }\]

\[\mathbf{находиться\ в\ точке\ }\]

\[\mathbf{пересечения\ серединных\ }\]

\[\mathbf{перпендикуляров\ к\ сторонам\ }\]

\[\mathbf{треугольника.}\]

\[\mathbf{Треугольник,\ вокруг\ которого\ }\]

\[\mathbf{описана\ окружность,\ }\]

\[\mathbf{называется\ вписанным\ в\ эту\ }\]

\[\mathbf{окружность.}\]

\[\boxed{\mathbf{22.}}\]

\[\mathbf{Теорема:}\]

\[\mathbf{около\ любого\ треугольника\ }\]

\[\mathbf{можно\ описать\ окружность,\ }\]

\[\mathbf{причем\ только\ одну.}\]

\[\mathbf{Дано:}\]

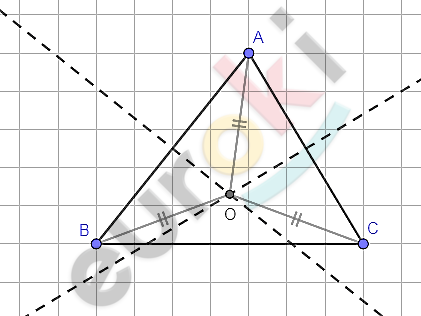
\[\mathbf{Доказать:\ \ }\]

\[\mathbf{о}коло\ любого\ треугольника\ \]

\[можно\ описать\ окружность\]

\[и\ только\ одну\text{.\ \ }\mathbf{\ }\]

\[\mathbf{Доказательство.}\]

\[1)\ Обозначим\ через\ \text{O\ }точку\ \]

\[пересечения\ серединных\ \]

\[перпендикуляров\ к\ сторонам\ \]

\[\text{AC\ }и\ \text{BC\ }данного\ треугольника.\]

\[2)\ По\ теореме\ о\ \]

\[геометрическом\ месте\ точек,\ \]

\[равноудаленных\ от\ двух\]

\[данных\ точек,\ точка\ \text{O\ }\]

\[равноудалена\ как\ от\ \]

\[вершин\ \text{A\ }и\ C,\ так\ и\ от\]

\[вершин\ \text{B\ }и\ \text{C.}\]

\[3)\ Значит,\ точка\ O\ \]

\[равноудалена\ от\ всех\ вершин\ \]

\[треугольника\ ABC,причем\ \]

\[точка\ O\ лежит\ на\ серединных\ \]

\[перпендикулярах\ к\ сторонам\ \]

\[\text{AC\ }и\ \text{BC.}\]

\[Значит,\ около\ любого\ \]

\[треугольника\ можно\ описать\ \]

\[окружность.\]

\[4)\ Так\ как\ серединные\ \]

\[перпендикуляры\ пересекаются\ \]

\[только\ в\ одной\ точке,\ то\ такая\ \]

\[окружность\ единственная.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{23.}}\]

\[\mathbf{Две\ точки,\ лежащие\ на\ одном\ }\]

\[\mathbf{перпендикуляре\ к\ данной\ }\]

\[\mathbf{прямой,\ по\ разные\ стороны\ и\ }\]

\[\mathbf{на\ одинаковом\ расстоянии\ }\]

\[\mathbf{от\ неё,\ называются\ }\]

\[\mathbf{симметричными\ относительно\ }\]

\[\mathbf{этой\ прямой.}\]

\[\boxed{\mathbf{24.}}\]

\[\mathbf{Фигура\ называется}\]

\[\mathbf{симметричной\ относительно\ }\]

\[\mathbf{если\ для\ каждой\ точки\ фигуры\ }\]

\[\mathbf{симметричная\ ей\ точка\ }\]

\[\mathbf{относительно\ прямой\ также\ }\]

\[\mathbf{принадлежит\ этой\ фигуре.\ }\]

\[\mathbf{При\ этом\ прямая\ называется\ }\]

\[\mathbf{осью\ симметрии\ фигуры.}\]

\[\boxed{\mathbf{25.}}\]

\[\mathbf{Две\ фигуры\ называются\ }\]

\[\mathbf{симметричными\ относительно\ }\]

\[\mathbf{прямой,\ если\ для\ любой\ точки\ }\]

\[\mathbf{одной\ фигуры\ симметричная\ }\]

\[\mathbf{ей\ }\left( \mathbf{относительно\ прямой} \right)\]

\[\mathbf{точка\ принадлежит\ другой\ }\]

\[\mathbf{фигуре.\ }\]

\[\boxed{\mathbf{26.}}\]

\[Чтобы\ построить\ точку,\ \]

\[симметричную\ некоторой\ \]

\[точке\ A\ относительно\]

\[прямой\ a,\ надо:\]

\[1)\ провести\ из\ точки\ \text{A\ }\]

\[к\ прямой\ перпендикуляр\ OA;\]

\[2)\ на\ продолжении\ \]

\[перпендикуляра,\ с\ другой\ \]

\[стороны\ от\ прямой\ a;\]

\[отложить\ отрезок\ OA_{1},\ равный\ \]

\[отрезку\ OA;\]

\[3)\ полученная\ точка\ A_{1}\ \]

\[симметрична\ точке\ A\ \]

\[относительно\ прямой\ \text{a.}\]

\[\boxed{\mathbf{27.}}\]

\[Чтобы\ построить\ ось\ \]

\[симметрии,\ двух\ данных\ точек,\ \]

\[надо:\]

\[1)\ соединить\ точки\ отрезком;\]

\[2)\ найти\ середину\ \]

\[полученного\ отрезка;\]

\[3)\ провести\ через\ нее\ \]

\[перпендикулярную\ прямую.\]

\[\boxed{\mathbf{28.}}\]

\[\mathbf{Нет.}\]

\[\mathbf{Если\ одна\ прямая\ пересекает\ }\]

\[\mathbf{ось\ симметрии,\ то\ и\ вторая\ }\]

\[\mathbf{должна\ пересекать\ ось\ }\]

\[\mathbf{симметрии,\ так\ как\ одна\ из\ }\]

\[\mathbf{точек\ первой\ прямой}\]

\[\mathbf{будет\ находиться\ на\ оси\ }\]

\[\mathbf{симметрии,\ и\ будет\ }\]

\[\mathbf{симметрична\ сама\ себе.}\]

\[\boxed{\mathbf{29.}}\]

\[\mathbf{Да,\ расстояния\ между\ }\]

\[\mathbf{симметричными\ точками\ }\]

\[\mathbf{равны,\ поэтому\ равны\ и\ }\]

\[\mathbf{расстояния.}\]

\[\boxed{\mathbf{30.}}\]

\[Построить\ точку,\ \]

\[симметричную\ точке\ M\ \]

\[относительно\ прямой\ b:\]

\[\textbf{а)}\ с\ помощью\ циркуля\ и\ \]

\[линейки.\]

\[1)\ провести\ перпендикуляр\ из\ \]

\[точки\ \text{M\ }к\ прямой\ b;отметить\ \]

\[в\ месте\ пересечения\ точку\ O;\]

\[2)\ с\ помощью\ циркуля\ из\ \]

\[точки\ пересечения\ прямой\ \]

\[с\ окружностью\ начертить\ \]

\[окружность,\ радиусом = MO;\]

\[3)\ на\ продолжении\ \]

\[перпендикуляра\ (в\ месте\ его\ \]

\[пересечения\ с\ окружностью)\ \ \]

\[отметить\ точку\ M_{1}.\]

\[\mathbf{б)\ с\ помощью\ одного\ циркуля.\ }\]

\[1)\ начертить\ окружность\ \]

\[произвольного\ радиуса\ \]

\[с\ центром\ в\ точке\ M\ так,\ чтобы\ \]

\[она\ пересекала\ прямую\ b;\]

\[2)\ обозначить\ точки\ \]

\[пересечения\ окружности\ \]

\[с\ прямой\ буквами:\]

\[например,\ \text{B\ }и\ C;\]

\[3)\ начертить\ окружности\ \]

\[с\ центрами\ в\ точках\ \text{B\ }и\ \text{C\ }\]

\[таким\ же\ радиусом,как\ и\ \]

\[первую\ окружность;\]

\[4)\ обозначить\ точку\ \]

\[пересечения\ окружностей\ \]

\[буквой\ M_{1}\text{.\ }\]