Решебник по геометрии 11 класс. Атанасян ФГОС Задачи для подготовки к ЕГЭ Задание 6

\[\boxed{\mathbf{Задание\ 6.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[\boxed{\mathbf{1.}}\]

\[⊿ABC;\ \ \angle C = 90{^\circ};\ \sin A = \frac{7}{25}\]

\[\sin B = \sin(90{^\circ} - A) = \cos A =\]

\[= \sqrt{1 - \sin^{2}A} = \sqrt{1 - \left( \frac{7}{25} \right)^{2}\ } =\]

\[= \frac{\sqrt{25^{2} - 7^{2}}}{25} = \frac{\sqrt{18 \cdot 32}}{25} =\]

\[= \frac{\sqrt{36 \cdot 16}}{25} = \frac{24}{25}.\]

\[Ответ:\ \frac{24}{25}.\]

\[\boxed{\mathbf{2.}}\]

\[⊿ABC;\ \ \angle C = 90{^\circ};BC = 6;\]

\[tg\ A = 0,5.\]

\[AC = AB \cdot \cos A;\ \ \]

\[BC = AC \cdot \sin A;\]

\[\frac{\text{BC}}{\text{AC}} = tg\ A\]

\[AC = \frac{\text{BC}}{\text{tg\ A}} = \frac{6}{0,5} = 12.\]

\[Ответ:12.\]

\[\boxed{\mathbf{3.}}\]

\[⊿ABC;\ \ \angle C = 90{^\circ};\ AB = 13;\]

\[tg\ A = 0,2 = \frac{1}{5};\]

\[CH - высота.\]

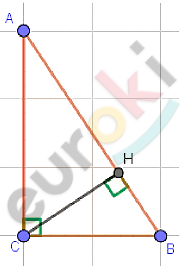
\[⊿ACB\ и\ ⊿AHC - подобны\ по\]

\[двум\ углам:\]

\[\angle ACB = \angle AHC = 90{^\circ};\]

\[\angle A - общий.\]

\[Отсюда:\]

\[\frac{\text{AB}}{\text{AC}} = \frac{\text{BC}}{\text{CH}}\]

\[CH = \frac{AC \cdot BC}{\text{AB}} =\]

\[= \frac{AB \cdot \cos A \cdot AB \cdot \sin A}{\text{AB}} =\]

\[= \frac{AB \cdot \sin{2A}}{2}.\]

\[\cos A = \frac{1}{\sqrt{1 + tg^{2}A}} = \frac{1}{\sqrt{1 + \frac{1}{25}}} =\]

\[= \frac{5}{\sqrt{26}};\]

\[\sin A = \cos A \cdot tg\ A = \frac{5}{\sqrt{26}} \cdot \frac{1}{5} =\]

\[= \frac{1}{\sqrt{26}};\]

\[\sin{2A} = 2\sin A\cos A =\]

\[= 2 \cdot \frac{1}{\sqrt{26}} \cdot \frac{5}{\sqrt{26}} = \frac{10}{26} = \frac{5}{13}.\]

\[Получаем:\]

\[CH = \frac{13 \cdot \frac{5}{13}}{2} = 2,5.\]

\[Ответ:2,5.\]

\[\boxed{\mathbf{4.}}\]

\[Дано:\]

\[⊿ABC;\]

\[AC = BC;\]

\[AB = 9,6;\]

\[\sin A = \frac{7}{25}.\]

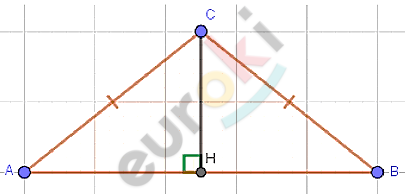
\[Решение.\]

\[1)\ Построим\ CH\bot AB.\]

\[2)\ ⊿ABC - равнобедренный:\]

\[CH - высота,\ медиана\ и\ \]

\[биссектриса.\]

\[AH = \frac{1}{2}AB = 4,8;\ \ \ \]

\[AH = AC \cdot \cos A\]

\[AC = \frac{\text{AH}}{\cos A};\]

\[\cos A = \sqrt{1 - \sin^{2}A} =\]

\[= \sqrt{1 - \frac{49}{625}} = \frac{24}{25} = \frac{96}{100} = 0,96;\]

\[AC = \frac{4,8}{0,96} = \frac{480}{96} = 5.\]

\[Ответ:5.\]

\[\boxed{\mathbf{5.}}\]

\[⊿ABC;AC = BC = 25;\ \ AB = 40.\]

\[CH - высота,\ медиана\ и\ \]

\[биссектриса:\]

\[AH = \frac{1}{2}AB = 20.\]

\[\cos A = \frac{\text{AH}}{\text{AC}} = \frac{20}{25} = \frac{4}{5};\]

\[\sin A = \sqrt{1 - \cos^{2}A} = \sqrt{1 - \frac{16}{25}} =\]

\[= \sqrt{\frac{9}{25}} = \frac{3}{5} = 0,6.\]

\[Ответ:0,6.\]

\[\boxed{\mathbf{6.}}\]

\[⊿ABC;\ \ \angle C = 90{^\circ};\ BH = 24;\]

\[CH = 7 - высота.\]

\[⊿ACB\ и\ ⊿CHB - подобны\ по\ \]

\[двум\ углам:\]

\[\angle ACB = \angle CHB = 90{^\circ};\]

\[\angle C - общий.\]

\[Отсюда:\]

\[\frac{\text{AC}}{\text{CH}} = \frac{\text{BC}}{\text{BH}}\]

\[\frac{\text{BC}}{\text{AC}} = \frac{\text{BH}}{\text{CH}}\]

\[\frac{\text{BC}}{\text{AC}} = tg\ A = \frac{24}{7};\]

\[\cos A = \frac{1}{\sqrt{1 + tg^{2}A}} =\]

\[= \frac{1}{\sqrt{1 + \left( \frac{24}{7} \right)^{2}}} = \frac{7}{\sqrt{7^{2} + 24^{2}}} =\]

\[= \frac{7}{\sqrt{625}} = \frac{7}{25} = \frac{28}{100} = 0,28.\]

\[Ответ:0,28.\]

\[\boxed{\mathbf{7.}}\]

\[⊿ABC;\ \ \angle C = 90{^\circ};tg\ A = \frac{24}{7};\]

\[\angle DBA - внешний\ угол\ при\ \]

\[вершине\ \text{B.}\]

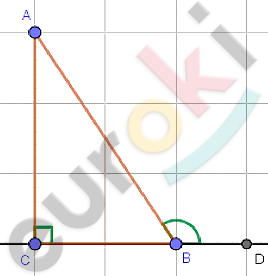
\[\cos{\angle DBA} = \cos(180{^\circ} - B) =\]

\[= - \cos B = - \cos(90{^\circ} - A) =\]

\[= - \sin A;\]

\[\cos A = \frac{1}{\sqrt{1 + tg^{2}A}} =\]

\[= \frac{1}{\sqrt{1 + \left( \frac{24}{7} \right)^{2}\ }} = \frac{7}{\sqrt{7^{2} + 24^{2}}} =\]

\[= \frac{7}{\sqrt{625}} = \frac{7}{25};\]

\[\sin A = \cos A \cdot tg\ A = \frac{7}{25} \cdot \frac{24}{7} =\]

\[= \frac{24}{25} = \frac{96}{100} = 0,96;\]

\[\cos{\angle DBA} = - 0,96.\]

\[Ответ:\ - 0,96.\]

\[\boxed{\mathbf{8.}}\]

\[ABCD - параллелограмм;\ \]

\[{\cos A = \frac{\sqrt{51}}{10}: }{Сумма\ смежных\ углов:}\]

\[\angle A + \angle B = 180{^\circ}\]

\[\sin B = \sin(180{^\circ} - A) = \sin A =\]

\[= \sqrt{1 - \cos^{2}A} =\]

\[= \sqrt{1 - \left( \frac{\sqrt{51}}{10} \right)^{2}} = \sqrt{\frac{49}{100}} = \frac{7}{10} =\]

\[= 0,7.\]

\[Ответ:0,7.\]

\[\boxed{\mathbf{9.}}\]

\[ABCD - трапеция;BC \parallel AD;\ \]

\[BC = 31;AD = 45;\]

\[AB = CD = 25.\]

\[Построим\ высоты:\]

\[BE\bot AD;\ \ CF\bot AD.\]

\[EBCF - прямоугольник.\]

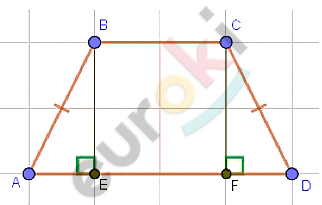
\[EF = BC = 31.\]

\[⊿AEB = ⊿DFC - по\ гипотенузе\ \]

\[и\ катету:\]

\[BE = CF;\]

\[AB = CD.\]

\[Отсюда:\]

\[AE = FD = \frac{AD - EF}{2} =\]

\[= \frac{45 - 31}{2} = 7;\]

\[\cos A = \frac{\text{AE}}{\text{AB}} = \frac{7}{25};\]

\[\sin A = \sqrt{1 - \cos^{2}A} =\]

\[= \sqrt{1 - \left( \frac{7}{25} \right)^{2}} = \frac{24}{25} = 0,96.\]

\[Ответ:0,96.\]

\[\boxed{\mathbf{10.}}\]

\[ABCD - трапеция;BC \parallel AD;\ \]

\[BC = 6;AD = 12;AB = CD;\]

\[\sin A = 0,8.\]

\[Построим\ высоты:\]

\[BE\bot AD;\ \ CF\bot AD.\]

\[EBCF - прямоугольник.\]

\[EF = BC = 31.\]

\[⊿AEB = ⊿DFC - по\ гипотенузе\ \]

\[и\ катету:\]

\[BE = CF;\]

\[AB = CD.\]

\[Отсюда:\]

\[AE = FD = \frac{AD - EF}{2} =\]

\[= \frac{12 - 6}{2} = 3;\]

\[AB = \frac{\text{AE}}{\cos A}\]

\[\cos A = \sqrt{1 - sin^{2}A} =\]

\[= \sqrt{1 - {0,8}^{2}} = 0,6.\]

\[AB = \frac{3}{0,6} = 5.\]

\[Ответ:5.\]

\[\boxed{\mathbf{11.}}\]

\[Достроим\ угол\ до\ \]

\[прямоугольника.\]

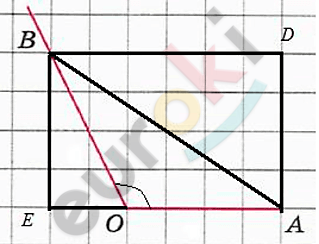
\[OA = 4;\]

\[OB = \sqrt{2^{2} + 4^{2}} = 2\sqrt{5};\]

\[AB = \sqrt{6^{2} + 4^{2}} = 2\sqrt{13}.\]

\[По\ теореме\ косинусов:\]

\[\cos O = \frac{OA^{2} + OB^{2} - AB^{2}}{2OA \cdot OB} =\]

\[= \frac{4^{2} + \left( 2\sqrt{5} \right)^{2} - \left( 2\sqrt{13} \right)^{2}}{2 \cdot 4 \cdot 2\sqrt{5}} =\]

\[= \frac{16 + 20 - 52}{16\sqrt{5}} = - \frac{1}{\sqrt{5}};\ - \ совьника.до\ \ ндикулярны\ и\ в\ енузы\ \]

\[\sin O = \sqrt{1 - \cos^{2}O} =\]

\[= \sqrt{1 - \left( - \frac{1}{\sqrt{5}} \right)^{2}} = \sqrt{1 - \frac{1}{5}} =\]

\[= \sqrt{\frac{4}{5}} = \frac{2}{\sqrt{5}};\ \]

\[\sqrt{5} \cdot \sin O = \sqrt{5} \cdot \frac{2}{\sqrt{5}} = 2.\]

\[Ответ:2.\]

\[\boxed{\mathbf{12.}}\]

\[\mathrm{\Delta}ABC;AB = BC;\ \ \angle 1 = 98{^\circ}.\]

\[Сумма\ углов\ треугольника\ \]

\[равна\ 180{^\circ};\]

\[2 \cdot 98{^\circ} = 196{^\circ} > 180{^\circ}.\]

\[Значит:\]

\[\angle 1 = 98{^\circ} - угол\ при\ вершине.\]

\[Углы\ при\ основании:\]

\[\angle 2 = \angle 3 = (180{^\circ} - 98{^\circ})\ :2 =\]

\[= 41{^\circ}.\]

\[Ответ:41{^\circ}.\]

\[\boxed{\mathbf{13.}}\]

\[⊿ABC;\ \ \]

\[AD - биссектриса;\ \ \angle C = 30{^\circ};\ \ \]

\[\angle BAD = 18{^\circ}.\]

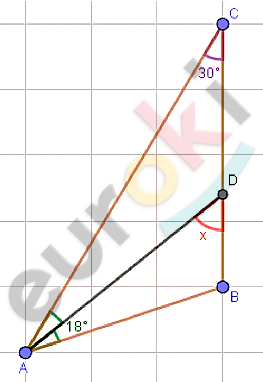
\[AD - биссектриса:\]

\[\angle CAD = \angle BAD = 18{^\circ}.\]

\[\angle ADB - внешний\ при\ вершине\ \]

\[\text{D\ }\left( для\ ⊿\text{ACD} \right):\]

\[\angle ADB = \angle CAD + \angle C =\]

\[= 18{^\circ} + 30{^\circ} = 48{^\circ}.\]

\[Ответ:48{^\circ}.\]

\[\boxed{\mathbf{14.}}\]

\[⊿ABC;\ \ \angle A = 58{^\circ};\ \angle B = 72{^\circ};\]

\[AA_{1};\ \ BB_{1} - высоты;\]

\[O - точка\ пересечения\ высот.\]

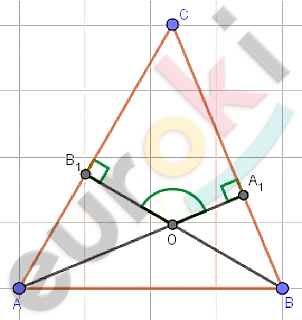
\[В\ треугольнике\ ABC:\]

\[\angle C = 180{^\circ} - (\angle A + \angle B) =\]

\[= 180{^\circ} - (58{^\circ} + 72{^\circ}) = 50{^\circ}.\]

\[В\ четырехугольнике\ OA_{1}CB_{1}:\]

\[\angle A_{1}OB_{1} =\]

\[= 360{^\circ} - (\angle C + 2 \cdot 90{^\circ}) =\]

\[= 360{^\circ} - 230{^\circ} = 130{^\circ}.\]

\[Ответ:130{^\circ}.\]

\[\boxed{\mathbf{15.}}\]

\[⊿ABC;\ \ \angle C = 90{^\circ};\ \]

\[AA_{1};\ \ BB_{1} - биссектрисы;\]

\[O - точка\ пересечения\ \]

\[биссектрис.\]

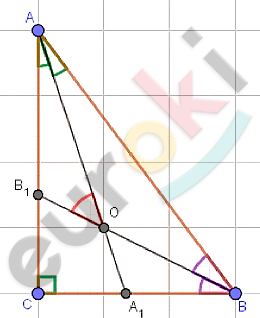
\[Пусть\ \angle A = \alpha;\]

\[\angle B = 90{^\circ} - \alpha.\]

\[\angle AOB_{1} - внешний\ угол\ при\ \]

\[вершине\ \text{O\ }\left( для\ ⊿\text{AOB} \right):\]

\[\angle AOB_{1} = \angle OAB + \angle OBA =\]

\[= \frac{\alpha}{2} + \frac{90{^\circ} - \alpha}{2} = 45{^\circ}.\]

\[Ответ:45{^\circ}.\]

\[\boxed{\mathbf{16.}}\]

\[⊿ABC;\ \ \angle C = 90{^\circ};\ \ \angle B > \angle A;\]

\[CH - высота;\]

\[CM - медиана;\]

\[\angle MCH = 20{^\circ}.\]

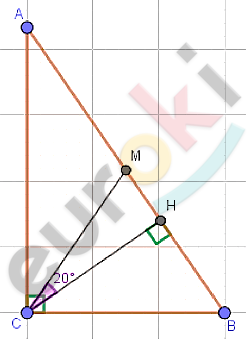
\[Пусть\ \angle A = \alpha;\ \ \angle B = 90{^\circ} - \alpha:\]

\[\angle BCH = 90{^\circ} - \angle B = \alpha;\]

\[\angle MCA =\]

\[= 90{^\circ} - (\angle MCH + \angle BCH) =\]

\[= 90{^\circ} - (20{^\circ} + \alpha) = 70{^\circ} - \alpha.\]

\[Точка\ M - центр\ вписанной\ \]

\[окружности:\]

\[MA = MC.\]

\[⊿AMC - равнобедренный\ с\ \]

\[основанием\ AC:\]

\[\angle A = \angle MCA.\]

\[Получаем:\]

\[\alpha = 70 - \alpha\]

\[2\alpha = 70\]

\[\alpha = 35{^\circ}.\]

\[\angle B = 90{^\circ} - \alpha = 90{^\circ} - 35{^\circ} = 55{^\circ}.\]

\[Ответ:55{^\circ}.\]

\[\boxed{\mathbf{17.}}\]

\[ABCD - ромб;AB = 2\sqrt{3};\ \ \]

\[\angle A = 60{^\circ};\]

\[AH - высота.\]

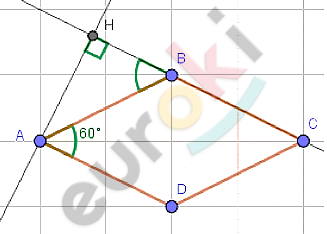
\[AD \parallel BC;AB - секущая:\]

\[\angle HBA = \angle A = 60{^\circ} - как\ \]

\[накрест\ лежащие.\]

\[В\ треугольнике\ AHB:\]

\[AH = AB \cdot \sin{\angle HBA} =\]

\[= 2\sqrt{3} \cdot \frac{\sqrt{3}}{2} = 3.\]

\[Ответ:3.\]

\[\boxed{\mathbf{18.}}\]

\[ABCD - трапеция;AD \parallel BC;\]

\[AD = 10;BC = 4;\]

\[KM - средняя\ линия.\]

\[1)\ AK = BK;\ \ KE \parallel BC:\]

\[KE - средняя\ линия\ ⊿ABC;\]

\[KE = \frac{1}{2}BC = 2.\]

\[2)\ Аналогично:\ \ \]

\[KF - средняя\ линия\ ⊿ABD;\]

\[KF = \frac{1}{2}AD = 5.\]

\[EM - средняя\ линия\ ⊿ACD:\]

\[EM = \frac{1}{2}AD = 5.\]

\[FM - средняя\ линия\ ⊿BCD:\]

\[FM = \frac{1}{2}BC = 2.\]

\[3)\ Получаем:\]

\[\max(KF;FM;KE;EM) =\]

\[= \max(5;2;2;5) = 5.\]

\[Ответ:5.\]

\[\boxed{\mathbf{19.}}\]

\[ABCD - трапеция;\ \ AD \parallel BC;\ \ \]

\[AD > BC;\]

\[AD = CD;\ \ AC\bot BD;\]

\[BH = 18 - высота;\]

\[KM - средняя\ линия.\]

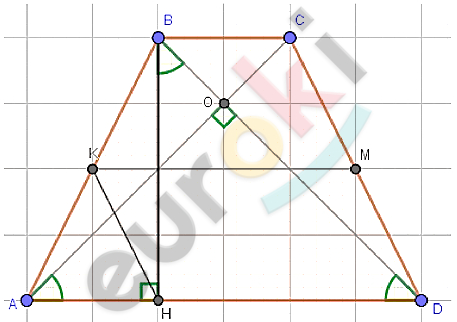
\[1)\ ⊿ABD = ⊿DCA - по\ двум\ \]

\[сторонам\ и\ углу\ между\ ними:\]

\[AB = CD;\]

\[AD - общая;\]

\[\angle A = \angle D.\]

\[Отсюда:\]

\[\angle BDA = \angle CAD.\]

\[2)\ O - точка\ пересечения\ \]

\[диагоналей\ \text{AC\ }и\ \text{BD.}\]

\[В\ ⊿AOD\ углы\ при\ основании\ \]

\[равны,\ а\ угол\ при\ вершине -\]

\[прямой:\]

\[\angle ODA = \angle OAD = 45{^\circ}.\]

\[3)\ В\ треугольнике\ BHD:\]

\[\angle BHD = 90{^\circ};\]

\[\angle BDH = 45{^\circ};\]

\[\angle DBH = 90 - 45 = 45{^\circ}.\]

\[⊿BHD - прямоугольный\ и\ \]

\[равнобедренный:\]

\[BH = HD.\]

\[4)\ ⊿AHB - прямоугольный:\]

\[середина\ гипотенузы\ K -\]

\[центр\ описанной\ окружности;\]

\[KA = KH = \frac{1}{2}AB = MD.\]

\[5)\ KM \parallel HD;\ \ KH = MD:\]

\[HKMD - параллелограмм;\]

\[HD = KM.\]

\[6)\ Получаем:\]

\[BH = HD = KM;\]

\[KM = 18.\]

\[Ответ:18.\]

\[\boxed{\mathbf{20.}}\]

\[Окружность\ (O;r);\ \]

\[AB - хорда;\ \ AB = r;\]

\[\angle ACB - вписанный.\]

\[⊿AOB - равносторонний:\]

\[AB = OA = OB = r.\]

\[\angle AOB = 60{^\circ} - центральный,\ \]

\[на\ хорде\ \text{AB.}\]

\[\angle ACB - вписан\ на\ хорде\ AB:\]

\[\angle ACB = \frac{1}{2}\angle AOB = \frac{1}{2} \cdot 60 = 30{^\circ}.\]

\[Ответ:30{^\circ}.\]

\[\boxed{\mathbf{21.}}\]

\[Окружность\ (O;R);\]

\[ABCD - вписанный\ \]

\[четырехугольник;\]

\[\angle A = 54{^\circ}.\]

\[Решение.\]

\[У\ вписанного\ \]

\[четырехугольника\ сумма\ \]

\[противоположных\ углов\ равна\ \]

\[180{^\circ}:\]

\[\angle C = 180{^\circ} - 54{^\circ} = 126{^\circ}.\]

\[Ответ:126{^\circ}.\]

\[\boxed{\mathbf{22.}}\]

\[⊿ABC - правильный;\ \ AB = \sqrt{3};\]

\[(O;r) - вписанная\ окружность.\]

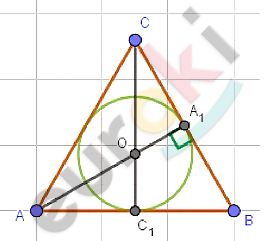
\[Решение.\]

\[В\ правильном\ треугольнике\ \]

\[центр\ вписанной\ окружности\ \]

\[совпадает\ с\ центром\ \]

\[треугольника.\]

\[O - точка\ пересечения\ медиан,\ \]

\[биссектрис\ и\ высот.\]

\[r = OA_{1} = \frac{1}{3}AA_{1} =\]

\[= \frac{1}{3}AB \cdot \sin{60{^\circ}} = \frac{1}{3} \cdot \sqrt{3} \cdot \frac{\sqrt{3}}{2} =\]

\[= \frac{3}{6} = \frac{1}{2} = 0,5.\]

\[Ответ:0,5.\]

\[\boxed{\mathbf{23.}}\]

\[ABCDEF - правильный\ \]

\[шестиугольник;AB = \sqrt{3};\]

\[(O;r) - вписанная\ окружность.\]

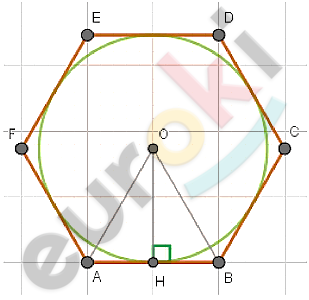
\[Решение.\]

\[В\ правильном\ шестиугольнике\ \]

\[центр\ вписанной\ окружности\ \]

\[совпадает\ с\ центром\ \]

\[шестиугольника.\]

\[⊿AOB - правильный:\]

\[OA = OB = AB;\]

\[OH\bot AB - высота.\]

\[r = OH = AB \cdot \sin{60{^\circ}} =\]

\[= \sqrt{3} \cdot \frac{\sqrt{3}}{2} = \frac{3}{2} = 1,5.\]

\[Ответ:1,5.\]

\[\boxed{\mathbf{24.}}\]

\[⊿ABC;\]

\[(O;R) - описанная\ \]

\[окружность;\]

\[\angle BAC = 23{^\circ}.\]

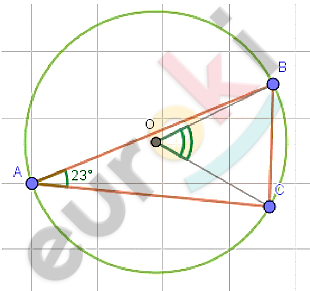
\[Решение.\]

\[\angle BOC - центральный\ угол\ на\ \]

\[хорде\ BC;\]

\[\angle BAC - вписанный\ угол\ на\ \]

\[хорде\ BC:\]

\[\angle BOC = 2\angle BAC = 2 \cdot 23 = 46{^\circ}.\]

\[Ответ:46{^\circ}.\]

\[\boxed{\mathbf{25.}}\]

\[⊿ABC;AB = BC = 5;AC = 6;\]

\[(O;r) - вписанная\ окружность.\]

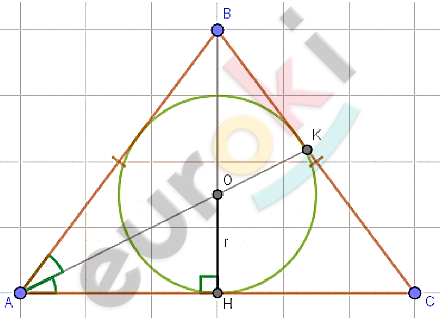
\[Решение.\]

\[1)\ Проведем\ BH\bot AC.\]

\[2)\ ⊿ABC - равнобедренный:\]

\[BH - высота,\ медиана\ и\ \]

\[биссектриса.\]

\[3)\ Проведем\ AK - биссектрису:\]

\[O - точка\ пересечения\ \text{BH\ }и\ \]

\[AK;или\ точка\ пересечения\ \]

\[биссектрис;\]

\[O - центр\ вписанной\ \]

\[окружности.\]

\[Отсюда:\]

\[OH\bot AC;H - точка\ касания\ \]

\[окружности\ и\ AC;\]

\[r = OH.\]

\[4)\ r = OH = AH \cdot tg\ \angle OAH =\]

\[= AH \cdot tg\frac{A}{2};\]

\[AH = \frac{\text{AC}}{2} = 3;\]

\[\cos A = \frac{\text{AH}}{\text{AB}} = \frac{3}{5} = 0,6;\]

\[tg^{2}A = \frac{1 - \cos A}{1 + \cos A} = \frac{1 - 0,6}{1 + 0,6} =\]

\[= \frac{0,4}{1,6} = \frac{1}{4};\]

\[tg\ A = \frac{1}{2}.\]

\[5)\ Получаем:\]

\[r = 3 \cdot \frac{1}{2} = 1,5.\]

\[Ответ:1,5.\]