Решебник по геометрии 11 класс. Атанасян ФГОС Задачи для подготовки к ЕГЭ Задание 8

\[\boxed{\mathbf{Задание\ 8.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[\boxed{\mathbf{1.}}\]

\[Прямоугольный\ \]

\[параллелепипед;\]

\[a = 3;b = 8;c = 5.\]

\[Квадрат\ диагонали\ \]

\[прямоугольного\ \]

\[параллелепипеда\ равен\]

\[сумме\ квадратов\ его\ \]

\[измерений:\]

\[d^{2} = 3^{2} + 8^{2} + 5^{2} =\]

\[= 9 + 64 + 25 = 98.\]

\[Ответ:98.\]

\[\boxed{\mathbf{2.}}\]

\[Прямоугольный\ \]

\[параллелепипед;\]

\[AB = 5;AD = 4;AA_{1} = 4.\]

\[\angle C_{1}BC - лежит\ в\ плоскости\ \]

\[грани\ \text{BC}C_{1}B_{1}:\]

\[BC = AD = 4;\ \ CC_{1} = AA_{1} = 4.\]

\[\text{BC}C_{1}B_{1} - квадрат:\]

\[BC_{1} - диагональ\ и\ биссектриса\ \]

\[прямоуго\ угла:\]

\[\angle C_{1}BC = 45{^\circ}.\]

\[Ответ:45{^\circ}.\]

\[\boxed{\mathbf{3.}}\]

\[SABC - правильная\ \]

\[треугольная\ пирамида;\]

\[S - вершина;\]

\[R - середина\ ребра\ BC;\]

\[AB = 1;\ \ SR = 2.\]

\[S_{бок} = 3S_{⊿}.\]

\[⊿SBC - равнобедренный:\]

\[SR - медиана,\ биссектриса\ и\ \]

\[высота\ боковой\ грани.\]

\[S_{⊿} = \frac{1}{2}BC \cdot SR = \frac{1}{2} \cdot 1 \cdot 2 = 1.\]

\[S_{бок} = 3 \cdot 1 = 3.\]

\[Ответ:3.\]

\[\boxed{\mathbf{4.}}\]

\[SABC - правильная\ \]

\[треугольная\ пирамида;\]

\[AA_{1};\ \ BB_{1};\ \ \ CC_{1} - медианы;\]

\[M - точка\ пересечения\ \]

\[медиан;\]

\[MS = 1;V = 1.\]

\[M - центр\ правильного\ ⊿ABC;\]

\[S - проецируется\ в\ M;\]

\[MS\bot\left( \text{ABC} \right);\]

\[MS - высота\ пирамиды.\]

\[V = \frac{1}{3} \cdot S_{\text{ABC}} \cdot MS\]

\[S_{\text{ABC}} = \frac{3V}{\text{MS}} = \frac{3 \cdot 1}{1} = 3.\]

\[Ответ:3.\]

\[\boxed{\mathbf{5.}}\]

\[Дано:\]

\[AC = 6;\]

\[SH\bot\left( \text{ABC} \right) - высота;\]

\[SH = 4.\]

\[Решение.\]

\[Вершина\ S - проецируется\ в\ \]

\[точку\ пересечения\ \]

\[диагоналей\ H:\]

\[AH = \frac{1}{2}AC = 3;\]

\[SA = \sqrt{SH^{2} + AH^{2}} =\]

\[= \sqrt{4^{2} + 3^{2}} = 5.\]

\[Ответ:5.\]

\[\boxed{\mathbf{6.}}\]

\[Дано:\]

\[a = 23.\]

\[Решение.\]

\[DF - малая\ диагональ\ \]

\[шестиугольника;\]

\[\angle E = 120{^\circ}.\]

\[По\ теореме\ косинусов:\]

\[DF^{2} =\]

\[= EF^{2} + ED^{2} - 2EF \cdot ED \cdot \cos{120{^\circ}} =\]

\[= a^{2} + a^{2} - 2a^{2} \cdot \left( - \frac{1}{2} \right) = 3a^{2}.\]

\[По\ теореме\ Пифагора:\]

\[DF_{1}^{2} = DF^{2} + EF_{1}^{2} =\]

\[= 3a^{2} + a^{2} = 4a^{2}\]

\[DF_{1} = \sqrt{4a²} = 2a = 2 \cdot 23 = 46.\]

\[Ответ:46.\]

\[\boxed{\mathbf{7.}}\]

\[Дано:\]

\[a = 49.\]

\[Решение.\]

\[AE - малая\ диагональ\ \]

\[шестиугольника;\]

\[\angle F = 120{^\circ}.\]

\[По\ теореме\ косинусов:\]

\[AE^{2} =\]

\[= AF^{2} + EF^{2} - 2AF \cdot EF \cdot \cos{120{^\circ}} =\]

\[= a^{2} + a^{2} - 2a^{2} \cdot \left( - \frac{1}{2} \right) = 3a^{2};\]

\[AE = a\sqrt{3}.\]

\[tg\angle E_{1}EA_{1} = \frac{\text{AE}}{EE_{1}} = \frac{a\sqrt{3}}{2a} = \sqrt{3};\]

\[\angle E_{1}EA_{1} = 60{^\circ}.\]

\[Ответ:60{^\circ}.\]

\[\boxed{\mathbf{8.}}\]

\[Конус;\]

\[h = 4;\ \ 2r = 6:\]

\[r = 3.\]

\[По\ теореме\ Пифагора\ \]

\[образующая\ конуса\ равна:\]

\[l = \sqrt{r^{2} + h^{2}} = \sqrt{3^{2} + 4^{2}} = 5.\]

\[Ответ:5.\]

\[\boxed{\mathbf{9.}}\]

\[Цилиндр;\]

\[S_{бок} = 2\pi;\ \ 2r = 1.\]

\[r = \frac{1}{2}:\]

\[S_{бок} = 2\pi rh = 2\pi\]

\[2\pi \cdot \frac{1}{2} \cdot h = 2\pi\]

\[h = 2\pi\ :\pi\]

\[h = 2.\]

\[Ответ:2.\]

\[\boxed{\mathbf{10.}}\]

\[Кубы;\]

\[b = 3a.\]

\[Отношение\ объемов:\]

\[\frac{V_{b}}{V_{a}} = \frac{b^{3}}{a^{3}} = \frac{(3a)^{3}}{a^{3}} = 3^{3} = 27.\]

\[Ответ:27.\]

\[\boxed{\mathbf{11.}}\]

\[Куб;\]

\[g = \sqrt{8} - диагональ\ грани.\]

\[Пусть\ ребро\ куба\ равно\ a:\]

\[g = a\sqrt{2}\]

\[a = \frac{g}{\sqrt{2}} = \frac{\sqrt{8}}{\sqrt{2}} = \sqrt{4} = 2.\]

\[V = a^{3} = 2^{3} = 8.\]

\[Ответ:8.\]

\[\boxed{\mathbf{12.}}\]

\[Прямоугольный\ \]

\[параллелепипед;\]

\[V = 60;\ \ S_{грани} = 12.\]

\[V = S \cdot a;где\ a\bot\left( \text{ABCD} \right):\]

\[a = \frac{V}{S} = \frac{60}{12} = 5.\]

\[Ответ:5.\]

\[\boxed{\mathbf{13.}}\]

\[Прямоугольный\ \]

\[параллелепипед;\]

\[a = 2;\ \ b = 6;\ \ V = 48:\]

\[V = abc\]

\[c = \frac{V}{\text{ab}} = \frac{48}{2 \cdot 6} = 4.\]

\[Ответ:4.\]

\[\boxed{\mathbf{14.}}\]

\[Прямоугольный\ ⊿ - основание\ \]

\[прямой\ треугольной\ призмы;\]

\(a = 6;\ \ b = 8;\ \ h = 5.\)

\[S_{осн} = \frac{1}{2}a \cdot b;\]

\[V = S_{осн} \cdot h = \frac{1}{2}a \cdot b \cdot h =\]

\[= \frac{1}{2} \cdot 6 \cdot 8 \cdot 5 = 120.\]

\[Ответ:120.\]

\[\boxed{\mathbf{15.}}\]

\[В\ основании\ призмы\ лежит\ \]

\[треугольник,\ средняя\ линия\ \]

\[проходит\ через\ середины\ двух\ \]

\[соседних\ сторон\ треугольника\ \]

\[и\ параллельна\ третьей\ \]

\[стороне.\ Длина\ средней\ линии\ \]

\[в\ 2\ раза\ меньше\ стороны,\ \]

\[которой\ она\ параллельна.\ \]

\[Таким\ образом,\ получаем,\ что\ \]

\[меньший\ треугольник\ \]

\[(основание\ отсеченной\ призмы)\]

\[имеет\ линейные\ размеры\ в\ \]

\[2\ раза\ меньшие,\ чем\ исходный\ \]

\[треугольник.\ \]

\[Следовательно,\ площадь\ \]

\[малого\ треугольника\ в\ 4\ раза\ \]

\[меньше\ площади\ исходного.\ \]

\[Высоты\ исходной\ и\ \]

\[отсеченной\ пирамид\ равны.\ \]

\[Получаем,\ что\ объем\ \]

\[отсеченной\ пирамиды\ \]

\[V_{2} = \frac{1}{4}S_{осн} \cdot \text{h\ \ }меньше\ \]

\[исходного\ объема\ V_{1} =\]

\[= S_{осн} \cdot h\ в\]

\[\frac{V_{2}}{V_{1}} = \frac{1}{4}\]

\[V_{2} = \frac{1}{4}V_{1}.\]

\[V_{1} = 32:\]

\[V_{2} = \frac{32}{4} = 8.\]

\[Ответ:8.\]

\[\boxed{\mathbf{16.}}\]

\[Правильная\ шестиугольная\ \]

\[призма;\]

\[a = 1 - сторона\ основания;\]

\[h = \sqrt{3} - боковое\ ребро.\]

\[Правильный\ шестиугольник\ \]

\[состоит\ из\ 6\ правильных\ \]

\[треугольников:\]

\[S_{1} = \frac{1}{2}a \cdot b \cdot \sin{60{^\circ}} =\]

\[= \frac{1}{2} \cdot 1 \cdot 1 \cdot \frac{\sqrt{3}}{2} = \frac{\sqrt{3}}{4};\]

\[S_{осн} = 6S_{1} = 6 \cdot \frac{\sqrt{3}}{4} = \frac{3\sqrt{3}}{2}.\]

\[V = S_{осн} \cdot h = \frac{3\sqrt{3}}{2} \cdot \sqrt{3} = \frac{9}{2} =\]

\[= 4,5.\]

\[Ответ:4,5.\]

\[\boxed{\mathbf{17.}}\]

\[Объем\ призмы:\]

\[V = S_{осн} \cdot \text{h.}\]

\[В\ основании\ призмы\ лежит\ \]

\[правильный\ шестиугольник\ \]

\[со\ сторонами\ 2.\ Его\ площадь\ \]

\[равна\ площади\ 6\ \]

\[равносторонним\ \]

\[треугольникам\ со\ сторонами\ 2.\]

\[Площадь\ одного\ треугольника:\]

\[S = \frac{1}{2}ab \cdot \sin{60{^\circ}} =\]

\[= \frac{1}{2} \cdot 2 \cdot 2 \cdot \frac{\sqrt{3}}{2} = \sqrt{3}.\]

\[Площадь\ основания:\]

\[S = 6S = 6\sqrt{3}.\]

\[Высота\ призмы:\]

\[h = 2\sqrt{3} \cdot \sin{30{^\circ}} = 2\sqrt{3} \cdot \frac{1}{2} =\]

\[= \sqrt{3}.\]

\[Объем\ призмы:\]

\[V = 6\sqrt{3} \cdot \sqrt{3} = 6 \cdot 3 = 18.\]

\[Ответ:18.\]

\[\boxed{\mathbf{18.}}\]

\[Дано:\]

\[боковое\ ребро = 3.\]

\[Решение.\]

\[В\ качестве\ основания\ \]

\[пирамиды\ выберем\ \]

\[треугольник\ ASB.\ \]

\[Тогда\ высотой\ пирамиды\ будет\ \]

\[выступать\ отрезок\ SC.\ \]

\[Площадь\ треугольника\ ASB\ \]

\[(то\ есть\ площадь\ основания):\]

\[S = \frac{1}{2}AS \cdot SB = \frac{1}{2} \cdot 3 \cdot 3 = \frac{9}{2}.\]

\[Объем\ пирамиды:\]

\[V = \frac{1}{3} \cdot S \cdot SC = \frac{1}{3} \cdot \frac{9}{2} \cdot 3 = \frac{9}{2} =\]

\[= 4,5.\]

\[Ответ:4,5.\]

\[\boxed{\mathbf{19.}}\]

\[Дано:\]

\[V = 16.\]

\[Решение.\]

\[V = \frac{1}{3}S_{осн} \cdot h;\]

\[S_{осн} = AD \cdot CD = 3 \cdot 4 = 12;\]

\[h = \frac{3V}{S_{осн}} = \frac{3 \cdot 16}{12} = 4.\]

\[Ответ:4.\]

\[\boxed{\mathbf{20.}}\]

\[Дано:\]

\[h = 12;\]

\[V = 200.\]

\[Решение.\]

\[V = \frac{1}{3}S_{осн} \cdot h\]

\[S_{осн} = \frac{3V}{h} = \frac{3 \cdot 200}{12} = 50.\]

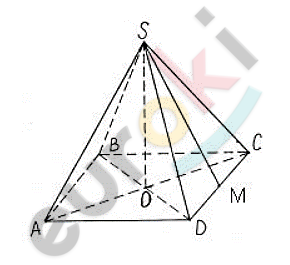
\[Так\ как\ в\ основании\ \]

\[правильной\ четырехугольной\ \]

\[пирамиды\ лежит\ квадрат,\ то\ \]

\[сторона\ квадрата\ будет\ равна:\]

\[a = \sqrt{S_{осн}} = \sqrt{50} = 5\sqrt{2}.\]

\[Вычислим\ диагональ\ по\ \]

\[теореме\ Пифагора:\]

\[d = \sqrt{a^{2} + a^{2}} = \sqrt{50 + 50} = 10.\]

\[Известно,\ что\ высота\ в\ \]

\[правильной\ пирамиде\ делит\ \]

\[диагонали\ пополам.\ \]

\[Следовательно,\ боковую\ грань\ \]

\[можно\ найти\ из\ \]

\[прямоугольного\ треугольника\ \]

\[AOS,\ где\ AO = 5,\ SO = 12:\]

\[AS = \sqrt{AO^{2} + SO^{2}} =\]

\[= \sqrt{25 + 144} = \sqrt{169} = 13.\]

\[Ответ:13.\]

\[\boxed{\mathbf{21.}}\]

\[Дано:\]

\[пирамида\ \text{ABC}C_{1}B_{1};\]

\[AB = 4;AD = 3;AA_{1} = 4.\]

\[Решение.\]

\[BB_{1}C_{1}C - основание\ \]

\[пирамиды:\]

\[V = S_{осн} \cdot \text{h.}\]

\[S_{осн} = BB_{1} \cdot BC;\]

\[h = A_{1}B_{1} = AB:\]

\[V = \frac{1}{3}BB_{1} \cdot BC \cdot AB =\]

\[= \frac{1}{3} \cdot 4 \cdot 3 \cdot 4 = 16.\]

\[Ответ:16.\]

\[\boxed{\mathbf{22.}}\]

\[Дано:\ \]

\[Решение.\]

\[Рассмотрим\ прямоугольный\ \]

\[треугольник\ ASH,\ в\ котором\]

\[высота\ SH = 6,\ угол\ SAH = 60{^\circ},\ \]

\[а\ угол\ ASH = 30{^\circ}.\ \]

\[Тогда\ отрезок\ AH\ будет\ равен:\]

\[tg\angle ASH = \frac{\text{AH}}{\text{SH}}\]

\[AH = SH \cdot tg\ 30{^\circ} = 6 \cdot \frac{\sqrt{3}}{3} =\]

\[= 2\sqrt{3}.\]

\[Треугольник\ ASD\ имеет\ два\ \]

\[угла\ по\ 60{^\circ}.\]

\[Следовательно,\ третий\ \]

\[угол\ ASD\ также\ равен\ 60{^\circ}\ и\ \]

\[треугольник\ ASD - \ \]

\[равносторонний.\ \]

\[В\ равностороннем\ \]

\[треугольнике\ высота\ SH\ делит\ \]

\[основание\ AD\ пополам,\ то\ есть\ \]

\[AD = 2AH\ и\ AD = 4\sqrt{3}.\]

\[Для\ нахождения\ второй\ \]

\[стороны\ основания\ \]

\[рассмотрим\ прямоугольный\ \]

\[треугольник\ SHG,\ в\ котором\ \]

\[угол\ SGH = 60{^\circ}\ по\ условию\ \]

\[задачи.\ \]

\[Следовательно,\ угол\ HSG\ будет\ \]

\[равен\ 30{^\circ}\ \]

\[Аналогично\ находим\ \]

\[длину\ HG:\]

\[HG = SH \cdot tg\ 30{^\circ} = 6 \cdot \frac{\sqrt{3}}{3} =\]

\[= 2\sqrt{3}.\]

\[S_{осн} = AD \cdot HG = 4\sqrt{3} \cdot 2\sqrt{3} =\]

\[= 24.\]

\[V = \frac{1}{3}S_{осн} \cdot h = \frac{1}{3} \cdot 24 \cdot 6 = 48.\]

\[Ответ:48.\]

\[\boxed{\mathbf{23.}}\]

\[Дано:\]

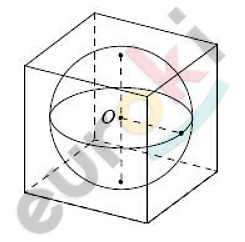
\[S_{пов} = 216.\]

\[Решение.\]

\[Площадь\ поверхности\ куба\ \]

\[равна:\]

\[S = 6a^{2};\ \ a - длина\ грани\ куба.\]

\[a = \sqrt{\frac{S}{6}} = \sqrt{\frac{216}{6}} = \sqrt{36} = 6.\]

\[Сфера\ вписана\ в\ куб,\ поэтому\ \]

\[ее\ радиус\ равен\ половине\ \]

\[длины\ ребра\ куба:\]

\[R = a\ :2 = 6\ :2 = 3.\]

\[Ответ:3.\]

\[\boxed{\mathbf{24.}}\]

\[Объем\ первого\ цилиндра:\]

\[V_{1} = S_{осн} \cdot h = \pi R^{2} \cdot h.\]

\[У\ второго\ цилиндра:\]

\[3h - высота;\]

\[\frac{R}{2} - радиус\ основания.\]

\[Его\ объем:\]

\[V_{2} = \pi \cdot \left( \frac{R}{2} \right)^{2} \cdot 3h = \frac{3}{4}\pi R^{2}\text{h.}\]

\[Получаем,\ что\ он\ в\ \frac{3}{4}\ раза\ \]

\[отличается\ от\ объема\ первого\ \]

\[цилиндра:\]

\[V_{2} = \frac{3}{4} \cdot 12 = 9.\]

\[Ответ:9.\]

\[\boxed{\mathbf{25.}}\]

\[Дано:\]

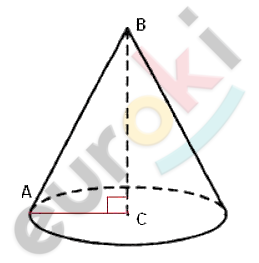
\[h = BC = 6;\]

\[l = AB = 10.\]

\[Решение.\]

\[\mathrm{\Delta}ABC - прямоугольный.\]

\[По\ теореме\ Пифагора:\]

\[r = AC = \sqrt{BC^{2} - AB^{2}} =\]

\[= \sqrt{100 - 36} = 8.\]

\[S_{осн} = \pi r^{2} = \pi \cdot 64.\]

\[V = \frac{1}{3}BC \cdot S_{осн} = \frac{1}{3} \cdot 6 \cdot 64\pi =\]

\[= 128\pi.\]

\[\frac{V}{\pi} = 128.\]

\[Ответ:128.\]

\[\boxed{\mathbf{26.}}\]

\[Дано:\]

\[d_{осн} = 6.\]

\[Решение.\]

\[Конус,\ у\ которого\ образующие\ \]

\[пересекаются\ под\ прямым\ \]

\[углом,\ вписывается\ в\ шар.\ \]

\[Причем,\ диаметр\ шара\ равен\ \]

\[диаметру\ основания\ конуса,\ а\ \]

\[радиус\ шара\ равен\ высоте\ \]

\[конуса,\ то\ есть\ высота\ конуса\ \]

\[равна:h = d\ :2 = 6\ :2 = 3.\]

\[V = \frac{1}{3}h \cdot S_{осн} = \frac{1}{3}h \cdot \pi \cdot \left( \frac{d}{2} \right)^{2} =\]

\[= \frac{1}{3} \cdot 3 \cdot \frac{36\pi}{4} = 9\pi.\]

\[\frac{V}{\pi} = \frac{9\pi}{\pi} = 9.\]

\[Ответ:9.\]

\[\boxed{\mathbf{27.}}\]

\[k = \frac{b}{a} = 2 - коэффициент\ \]

\[подобия\ кубов.\]

\[\frac{S_{2}}{S_{1}} = k^{2} = 4\ (раза) -\]

\[увеличится\ площадь.\]

\[Ответ:в\ 4\ раза.\]

\[\boxed{\mathbf{28.}}\]

\[k = \frac{b}{a} = \frac{1}{4} - коэффициент\ \]

\[подобия\ тетраэдров.\]

\[\frac{S_{2}}{S_{1}} = k^{2} = \frac{1}{16} - отношение\ \]

\[площадей.\]

\[S_{2} = \frac{1}{16}S_{1} = \frac{80}{16} = 5\ см^{2}.\]

\[Ответ:5\ см^{2}.\]

\[\boxed{\mathbf{29.}}\]

\[S_{1} = \pi r_{1}l_{1};\ \ \ \ S_{2} = \pi r_{2}l_{2}:\]

\[\frac{S_{2}}{S_{1}} = \frac{\pi r_{1}l_{1}}{\pi r_{2}l_{2}} = \frac{\frac{r_{1}}{4} \cdot 2l_{1}}{r_{1}l_{1}} = \frac{1}{2};\]

\[S_{2} = \frac{1}{2}S_{1} = \frac{1}{2} \cdot 16 = 8\ \left( см^{2} \right).\]

\[Ответ:8\ см^{2}.\]