Решебник по геометрии 11 класс. Атанасян ФГОС Задачи для подготовки к ЕГЭ Задание 3

\[\boxed{\mathbf{Задание\ 3.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[\boxed{\mathbf{1.}}\]

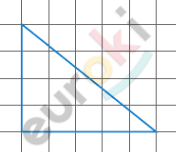
\[S = \frac{1}{2} \cdot 4 \cdot 5 = 10\ см^{2}\text{.\ }\]

\[Ответ:10\ см^{2}.\]

\[\boxed{\mathbf{2.}}\]

\[Достроим\ треугольник\ до\ \]

\[прямоугольного:\]

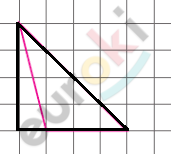
\[Получим:\]

\[S = \frac{1}{2} \cdot 4 \cdot 4 - \frac{1}{2} \cdot 4 \cdot 1 = 8 - 2 =\]

\[= 6\ см^{2}.\]

\[Ответ:6\ см^{2}.\]

\[\boxed{\mathbf{3.}}\]

\[Достроим\ треугольник\ до\ \]

\[прямоугольника:\]

\[Получим:\]

\[S =\]

\[= 6 \cdot 4 - \frac{1}{2} \cdot 4 \cdot 2 - \frac{1}{2} \cdot 4 \cdot 2 - \frac{1}{2} \cdot 6 \cdot 2 =\]

\[= 24 - 4 - 4 - 6 = 10\ см^{2}.\]

\[Ответ:10\ см^{2}.\]

\[\boxed{\mathbf{4.}}\]

\[Достроим:\]

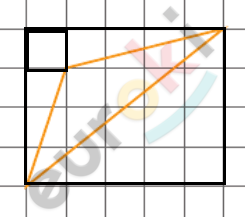
\[Получим:\]

\[Ответ:5,5\ см^{2}.\]

\[\boxed{\mathbf{5.}}\]

\[Разобьем\ на\ две\ фигуры:\]

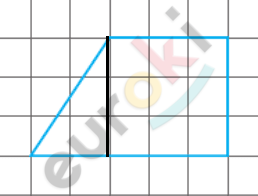
\[Получим:\]

\[S = \frac{1}{2} \cdot 2 \cdot 3 + 3 \cdot 3 = 3 + 9 =\]

\[= 12\ см^{2}.\]

\[Ответ:12\ см^{2}.\]

\[\boxed{\mathbf{6.}}\]

\[Разобьем\ на\ три\ фигуры:\]

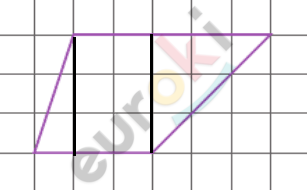
\[S = \frac{1}{2} \cdot 3 \cdot 1 + 2 \cdot 3 + \frac{1}{2} \cdot 3 \cdot 3 =\]

\[= 6 + 1,5 + 4,5 = 12\ см^{2}.\]

\[Ответ:12\ см^{2}.\]

\[\boxed{\mathbf{7.}}\]

\[Разобьем\ на\ три\ фигуры:\]

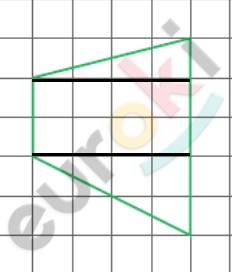
\[S = \frac{1}{2} \cdot 4 \cdot 1 + 4 \cdot 2 + \frac{1}{2} \cdot 2 \cdot 4 =\]

\[= 2 + 8 + 4 = 14\ см^{2}.\]

\[Ответ:14\ см^{2}.\]

\[\boxed{\mathbf{8.}}\]

\[Дополним:\]

\[Ответ:10\ см^{2}.\]

\[\boxed{\mathbf{9.}}\]

\[Дополним:\]

\[S = 4 \cdot 4 - 4 \cdot \frac{1}{2} \cdot 3 \cdot 1 =\]

\[= 16 - 6 = 10\ см^{2}.\]

\[Ответ:10\ см^{2}.\]

\[\boxed{\mathbf{10.}}\]

\[\angle AOB = 90{^\circ}:\]

\[\cup ACB = 360{^\circ} - 90{^\circ} = 270{^\circ}.\]

\[S = \frac{270{^\circ}}{360{^\circ}} \cdot S_{кр} = \frac{3}{4}\pi R^{2}.\]

\[R = OC = 4\ см.\]

\[\frac{S}{\pi} = \frac{3}{4}R^{2} = \frac{3}{4} \cdot 4^{2} = 12\ см^{2}.\]

\[Ответ:12\ см^{2}.\]

\[\boxed{\mathbf{11.}}\]

\[S = a^{2} = 2\]

\[a = \sqrt{2}:\]

\[d = \sqrt{\left( \sqrt{2} \right)^{2} + \left( \sqrt{2} \right)^{2}} = \sqrt{2 + 2} =\]

\[= 2.\]

\[Ответ:диагональ\ равна\ 2.\]

\[\boxed{\mathbf{12.}}\]

\[a = 8;\ \ b = 12;\ \ \]

\[\angle(a;b) = 150{^\circ}.\]

\[S = \frac{1}{2}ab \cdot \sin{150{^\circ}} =\]

\[= \frac{1}{2} \cdot 8 \cdot 12 \cdot \sin{30{^\circ}} = 48 \cdot \frac{1}{2} =\]

\[= 24.\]

\[Ответ:24.\]

\[\boxed{\mathbf{13.}}\]

\[a = 6;\ \ b = 8;\]

\[\angle(a;b) = 30{^\circ}.\]

\[S = a \cdot b \cdot \sin{30{^\circ}} = 6 \cdot 8 \cdot \frac{1}{2} =\]

\[= 24.\]

\[Ответ:24.\]

\[\boxed{\mathbf{14.}}\]

\[S = 12;\ \ a = 6.\]

\[S = \frac{1}{2}a \cdot b = 12\]

\[\frac{1}{2} \cdot 6 \cdot b = 12\]

\[b = 12\ :3\]

\[b = 4.\]

\[Ответ:второй\ катет\ равен\ 4.\]

\[\boxed{\mathbf{15.}}\]

\[a = 3;\ \ b = 1;\ \ h = 1:\]

\[S = \frac{a + b}{2} \cdot h = \frac{3 + 1}{2} \cdot 1 = 2.\]

\[Ответ:2.\]

\[\boxed{\mathbf{16.}}\]

\[P_{1}\ :P_{2} = 3\ :5\]

\[S_{1} = 36.\]

\[Отношение\ периметров:\]

\[k = \frac{3}{5}.\]

\[Отношение\ площадей:\]

\[\frac{S_{1}}{S_{2}} = k^{2} = \frac{9}{25};\]

\[S_{2} = 36 \cdot \frac{25}{9} = 100.\]

\[Ответ:100.\]

\[\boxed{\mathbf{17.}}\]

\[C = \sqrt{\pi}.\]

\[Длина\ окружности:\]

\[C = 2\pi R\]

\[R = \frac{C}{2\pi} = \frac{\sqrt{\pi}}{2\pi} = \frac{1}{2\sqrt{\pi}}.\]

\[Площадь\ круга:\]

\[S = \pi R^{2} = \pi \cdot \left( \frac{1}{2\sqrt{\pi}} \right)^{2} = \pi \cdot \frac{1}{4\pi} =\]

\[= \frac{1}{4} = 0,25.\]

\[Ответ:0,25.\]

\[\boxed{\mathbf{18.}}\]

\[R = 1;\ \ C_{\cup} = 2.\]

\[C_{\cup} = \frac{\alpha}{2\pi} \cdot 2\pi R = \alpha R;\]

\[\alpha = \frac{C_{\cup}}{R};\]

\[\alpha - центральный\ угол\ в\ \]

\[радианах.\]

\[Площадь\ сектора:\]

\[S = \frac{\alpha}{2\pi} \cdot \pi R^{2} = \frac{\alpha R^{2}}{2} = \frac{C_{\cup}}{R} \cdot \frac{R^{2}}{2} =\]

\[= \frac{C_{\cup} \cdot R}{2} = \frac{2 \cdot 1}{2} = 1.\]

\[Ответ:1.\]

\[\boxed{\mathbf{19.}}\]

\[Пусть\ x - одна\ сторона\ \]

\[прямоугольника;\]

\[(x - 2) - другая\ сторона.\]

\[Известно,\ что\ периметр\ \]

\[равен\ 16.\]

\[Составим\ уравнение:\]

\[2 \cdot (x + x - 2) = 16\]

\[2x - 2 = 8\]

\[2x = 10\]

\[x = 5\ (см) - одна\ сторона\ \]

\[прямоугольника.\]

\[x - 2 = 5 - 2 = 3\ (см) - другая\ \]

\[сторона.\]

\[S = 5 \cdot 3 = 15\ см^{2}.\]

\[Ответ:15\ см^{2}.\]

\[\boxed{\mathbf{20.}}\]

\[34\ :2 = 17 - сумма\ длин\ двух\ \]

\[сторон.\]

\[Пусть\ x - одна\ сторона\ \]

\[прямоугольника;\]

\[(17 - x) - другая\ сторона.\]

\[Площадь\ равна\ 60.\]

\[Составим\ уравнение:\]

\[x(17 - x) = 60\]

\[17x - x^{2} - 60 = 0\]

\[x^{2} - 17x + 60 = 0\]

\[x_{1} + x_{2} = 17;\ \ \ x_{1} \cdot x_{2} = 60\]

\[x_{1} = 12;\ \ \ x_{2} = 5.\]

\[12\ и\ 5 - стороны\ \]

\[прямоугольника.\]

\[По\ теореме\ Пифагора\ найдем\ \]

\[его\ диагональ:\]

\[d = \sqrt{12^{2} + 5^{2}} = \sqrt{144 + 25} =\]

\[= \sqrt{169} = 13.\]

\[Ответ:13.\]

\[\boxed{\mathbf{21.}}\]

\[a = 9;\ \ b = 15;\]

\[h_{a} = 10;\ \ h_{b} - ?\]

\[S = a \cdot h_{a} = b \cdot h_{b}\]

\[9 \cdot 10 = 15 \cdot h_{b}\]

\[h_{b} = 90\ :15\]

\[h_{b} = 6.\]

\[Ответ:6.\]

\[\boxed{\mathbf{22.}}\]

\[P = 12;\ \ r = 1.\]

\[S = \frac{1}{2} \cdot P \cdot r = \frac{1}{2} \cdot 12 \cdot 1 = 6.\]

\[Ответ:6.\]

\[\boxed{\mathbf{23.}}\]

\[a = 2;\ \ b = 8;\ \ S = 30.\]

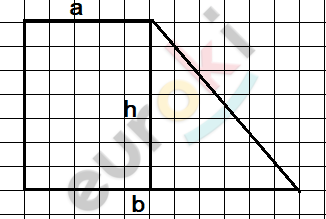
\[S = \frac{a + b}{2} \cdot h\]

\[h = \frac{2S}{a + b} = \frac{2 \cdot 30}{8 + 2} = 6.\]

\[b - a = 8 - 2 = 6;\]

\[h = b - a:\]

\[получившися\ \mathrm{\Delta} -\]

\[равнобедренный.\]

\[Значит,\ острый\ угол\ \alpha:\]

\[\alpha = 90{^\circ}\ :2 = 45{^\circ}.\]

\[Ответ:45{^\circ}.\]

\[\boxed{\mathbf{24.}}\]

\[A(5;9).\]

\[При\ симметрии\ относительно\ \]

\[Oy:\]

\[A_{1}( - 5;9)\text{.\ }\]

\[Ответ:x_{1} = - 5.\]

\[\boxed{\mathbf{25.}}\]

\[A(3;7);\ \ B( - 1;3).\]

\[Ордината\ середины\ отрезка:\]

\[y = \frac{7 + 3}{2} = 5.\]

\[Ответ:y = 5.\]

\[\boxed{\mathbf{26.}}\]

\[\overrightarrow{a}\left\{ 6;8 \right\}:\]

\[\left| \overrightarrow{a} \right| = \sqrt{6^{2} + 8^{2}} = \sqrt{100} = 10.\]

\[Ответ:10.\]

\[\boxed{\mathbf{27.}}\]

\[A(3;0);\ \ B(0;3):\]

\[\frac{x - 3}{0 - 3} = \frac{y - 0}{3 - 0}\]

\[- (x - 3) = y\]

\[Уравнение\ прямой:\]

\[y = - x + 3.\]

\[k = - 1.\]

\[Ответ:\ - 1.\]

\[\boxed{\mathbf{28.}}\]

\[O(0;0);A(8;6);B(12; - 2).\]

\[\overrightarrow{\text{BO}} = \overrightarrow{\text{AC}} = \overrightarrow{a}\]

\[\overrightarrow{\text{BO}} = \left\{ 0 - 12;0 + 2 \right\} = \left\{ - 12;2 \right\}.\]

\[a_{x} = - 12;\ \ a_{y} = 2.\]

\[x_{C} = x_{A} + a_{x} = 8 - 12 = - 4;\]

\[y_{C} = y_{A} + a_{y} = 6 + 2 = 8.\]

\[Ответ:8.\]

\[\boxed{\mathbf{29.}}\]

\[3x + 2y = 6;\ \ при\ y = 0:\]

\[3x + 2 \cdot 0 = 6\]

\[3x = 6\]

\[x = 2.\]

\[Ответ:x = 2.\]

\[\boxed{\mathbf{30.}}\]

\[3x + 2y = 6;\ \ y = - x:\]

\[2y = 6 - 3x\]

\[y = 3 - 1,5x.\]

\[Получаем:\]

\[3 - 1,5x = - x\]

\[0,5x = 3\]

\[x = 6.\]

\[y = - x = - 6.\]

\[Ответ:\ - 6.\]

\[\boxed{\mathbf{31.}}\]

\[P(5;7) - центр\ окружности.\]

\[r\bot Ox:\]

\[x = x_{P} = 7.\]

\[(7;0) - точка\ касания\ оси\ \text{Ox.}\]

\[Найдем\ радиус\ окружности:\]

\[r = \sqrt{(7 - 7)^{2} + (5 - 0)^{2}} =\]

\[= \sqrt{25} = 5.\]

\[Ответ:5.\]

\[\boxed{\mathbf{32.}}\]

\[⊿ABC;\ \ \]

\[A(6;0);B(0;10);C(6;10).\]

\[P\left( x_{p};y_{p} \right) - центр\ описанной\ \]

\[окружности.\]

\[\overrightarrow{\text{CA}} = \left\{ 6 - 6;10 - 0 \right\} = \left\{ 0;10 \right\};\]

\[\overrightarrow{\text{CB}} = \left\{ 0 - 6;10 - 10 \right\} = \left\{ - 6;0 \right\};\]

\[\overrightarrow{\text{CA}} \cdot \overrightarrow{\text{CB}} = 0 \cdot ( - 6) + 10 \cdot 0 = 0.\]

\[\overrightarrow{\text{CA}}\bot\overrightarrow{\text{CB}}:\]

\[⊿\text{ABC} - прямоугольный;\]

\[центр\ описанной\ окружности -\]

\[середина\ гипотенузы\ \text{AB.}\]

\[x_{p} = \frac{6 + 0}{2} = 3;\ \ \ y_{p} = \frac{0 + 10}{2} =\]

\[= 5.\]

\[Ответ:3.\]

\[\boxed{\mathbf{33.}}\]

\[⊿ABC;\ \ \]

\[A(1;1);B(4;3);C(4;5).\]

\[Достроим:\]

\[Получим:\]

\[S = \frac{1}{2} \cdot 3 \cdot 4 - \frac{1}{2} \cdot 2 \cdot 3 = 6 - 3 =\]

\[= 3.\]

\[Ответ:3.\]

\[\boxed{\mathbf{34.}}\]

\[ABCD - прямоугольник;\]

\[AB = 6;\ \ AD = 8.\]

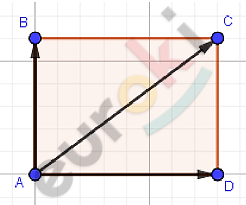
\[По\ правилу\ параллелограмма:\]

\[\overrightarrow{\text{AB}} + \overrightarrow{\text{AD}} = \overrightarrow{\text{AB}} + \overrightarrow{\text{BC}} = \overrightarrow{\text{AC}}.\]

\[Длина\ суммы\ векторов\ равна\ \]

\[длине\ диагонали:\]

\[\left| \overrightarrow{\text{AB}} + \overrightarrow{\text{AD}} \right| = \left| \overrightarrow{\text{AC}} \right| = AC =\]

\[= \sqrt{AB^{2} + AD^{2}} = \sqrt{6^{2} + 8^{2}} =\]

\[= 10.\]

\[Ответ:10.\]

\[\boxed{\mathbf{35.}}\]

\[ABCD - ромб;\]

\[AC = 12;\ \ BD = 16.\]

\[\overrightarrow{\text{AB}} = \overrightarrow{\text{AO}} + \overrightarrow{\text{OB}}\]

\[Диагонали\ ромба\ \]

\[перпендикулярны\ и\ в\ точке\ \]

\[пересечения\ делятся\ пополам:\]

\[AO = \frac{\text{AC}}{2} = \frac{12}{2} = 6;\ \ \ \]

\[OB = \frac{\text{BD}}{2} = \frac{16}{2} = 8.\]

\[\left( \overrightarrow{\text{AB}} \right)^{2} =\]

\[= \left( \overrightarrow{\text{AO}} \right)^{2} + \left( \overrightarrow{\text{OB}} \right)^{2} + 2\overrightarrow{\text{AO}} \cdot \overrightarrow{\text{OB}} =\]

\[= AO^{2} + OB^{2} + 2AO \cdot OB \cdot \cos{90{^\circ}} =\]

\[= AO^{2} + OB^{2} = 6^{2} + 8^{2} = 10^{2}\]

\[\left| \overrightarrow{\text{AB}} \right| = 10.\]

\[Ответ:10.\]

\[\boxed{\mathbf{36.}}\]

\[ABCD - ромб;\]

\[AC = 12;BD = 16.\]

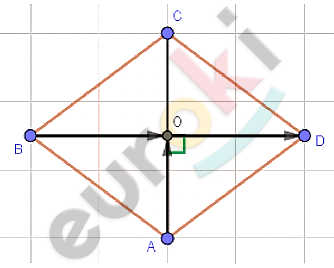
\[Диагонали\ ромба\ \]

\[перпендикулярны\ и\ в\ точке\ \]

\[пересечения\ делятся\ пополам:\]

\[AO = \frac{\text{AC}}{2} = \frac{12}{2} = 6;\ \ \]

\[BO = \frac{\text{BD}}{2} = \frac{16}{2} = 8.\]

\[\overrightarrow{\text{BO}} = \overrightarrow{\text{OD}};\]

\[\angle\left( \overrightarrow{\text{AO}};\overrightarrow{\text{BO}} \right) = \angle\left( \overrightarrow{\text{AO}};\overrightarrow{\text{OD}} \right) = 90{^\circ};\]

\[\overrightarrow{\text{AO}} \cdot \overrightarrow{\text{BO}} = AO \cdot BO \cdot \cos{90{^\circ}} = 0.\]

\[Ответ:0.\]

\[\boxed{\mathbf{37.}}\]

\[⊿ABC - равносторонний;\]

\[AB = \sqrt{3}.\]

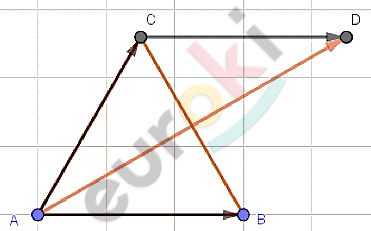
\[Проведем\ \overrightarrow{\text{CD}} = \overrightarrow{\text{AB}}:\]

\[ACDB - параллелограмм.\]

\[По\ правилу\ параллелограмма:\]

\[\overrightarrow{\text{AB}} + \overrightarrow{\text{AC}} = \overrightarrow{\text{AC}} + \overrightarrow{\text{CD}} = \overrightarrow{\text{AD}}\]

\[\left| \overrightarrow{\text{AB}} + \overrightarrow{\text{AC}} \right| = \left| \overrightarrow{\text{AD}} \right| = AD;\]

\[\angle ACD = 180{^\circ} - \angle A = 120{^\circ};\]

\[\cos{120{^\circ}} = - \cos(180{^\circ} - 120{^\circ}) =\]

\[= - \cos{60{^\circ}} = - \frac{1}{2}.\]

\[По\ теореме\ косинусов:\]

\[AD^{2} =\]

\[= AC^{2} + CD^{2} - 2AC \cdot CD \cdot \cos{\angle ACD} =\]

\[= \left( \sqrt{3} \right)^{2} + \left( \sqrt{3} \right)^{2} - 2\sqrt{3} \cdot \sqrt{3} \cdot \left( - \frac{1}{2} \right) =\]

\[= 9\]

\[AD = \sqrt{9} = 3.\]

\[Ответ:3.\]

\[\boxed{\mathbf{38.}}\]

\[⊿ABC - равносторонний;\]

\[AB = 1.\]

\[Решение.\]

\[Все\ углы\ ⊿\text{ABC}\ равны\ 60{^\circ}.\]

\[\overrightarrow{\text{AB}} \cdot \overrightarrow{\text{AC}} = AB \cdot AC \cdot \cos{60{^\circ}} =\]

\[= 1 \cdot 1 \cdot \frac{1}{2} = \frac{1}{2} = 0,5.\]

\[Ответ:0,5.\]