Решебник по геометрии 11 класс. Атанасян ФГОС 759

\[\boxed{\mathbf{759.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[\angle\left( \text{CABD} \right) = \varphi < 90{^\circ};\]

\[AC\bot AB;\]

\[\angle DAB = \theta.\]

\[Найти:\]

\[\cos{\angle CAD}.\]

\[Решение.\]

\[1)\ Из\ точки\ A\ проведем\ \]

\[OA\bot AB:\]

\[\angle CAO = \text{φ.}\]

\[2)\ Отложим\ AC = AO.\]

\[Проведем\ отрезок\ CO;из\ точки\ \]

\[\text{O\ }проведем\ луч,\ пересекающий\ \]

\[луч\ \text{AD}\]

\[в\ точке\ D:\ \ \ OD \parallel AB.\]

\[3)\ Так\ как\ OD \parallel AB;OA\bot AB:\]

\[OD\bot OA.\]

\[4)\ По\ теореме\ о\ трех\ \]

\[перпендикулярах:\]

\[CO\bot OD.\]

\[5)\ Пусть\ AD = a.\]

\[AO = a \cdot \sin\theta;\]

\[OD = a \cdot \cos\theta.\]

\[6)\ В\ треугольнике\ OAC\ \]

\[(по\ теореме\ косинусов):\]

\[CO^{2} =\]

\[= OA^{2} + AC^{2} - 2AC \cdot AO \cdot \cos\varphi\]

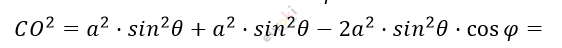
\[= 2a^{2} \cdot \sin^{2}\theta \cdot \left( 1 - cos^{2}\varphi \right).\]

\[7)\ ⊿COD - прямоугольный:\]

\[CD^{2} = OC^{2} + OD^{2}\]

\[CD^{2} =\]

\[= 2a^{2} \cdot \sin^{2}\theta \cdot \left( 1 - cos^{2}\varphi \right) + a^{2}\text{co}s^{2}\text{θ.}\]

\[8)\ По\ теореме\ косинусов\ в\ \]

\[⊿\text{CAD\ }(\angle CAD = x):\]

\[CD^{2} =\]

\[= CA^{2} + AD^{2} - 2 \cdot CA \cdot AD \cdot \cos x\]

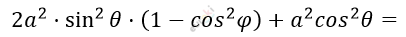
\[= a^{2} \cdot \sin^{2}\theta + a^{2} - 2a^{2}\sin\theta \cdot \cos x\]

\[2sin^{2}\theta - 2sin^{2}\theta\cos\varphi + cos^{2}\theta =\]

\[= sin^{2}\theta + 1 - 2\sin\theta\cos x\]

\[\text{si}n^{2}\theta - 2sin^{2}\theta\cos\varphi + cos^{2}\theta - 1 =\]

\[= - 2\sin\theta\cos x\]

\[1 - 2sin^{2}\theta\cos\varphi - 1 =\]

\[= - 2\sin\theta\cos x\]

\[2sin^{2}\theta\cos\varphi = 2\sin\theta\cos x\]

\[\sin\theta \neq 0:\]

\[\sin\theta\cos\varphi = \cos x;\]

\[\cos{\angle CAD} = \sin\theta\cos\varphi.\]

\[Ответ:\ \sin\theta\cos\varphi.\]