Решебник по геометрии 11 класс. Атанасян ФГОС 331

\[\boxed{\mathbf{331.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

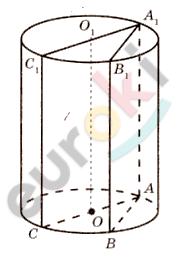
\[h - высота;\]

\[\angle BAC = \varphi - линейный\ угол\ \]

\[двугранного\ угла\ \text{CA}A_{1}B;\]

\[R - радиус\ основания.\]

\[Найти:\]

\[\frac{S_{1}}{S_{2}}.\]

\[Решение.\]

\[S_{1} = S_{A_{1}C_{1}\text{CA}} = 2R \cdot H.\]

\[По\ теореме\ синусов:\]

\[\frac{\text{AB}}{\sin(180{^\circ} - 2\varphi)} = \frac{R}{\sin\varphi}\]

\[\frac{\text{AB}}{\sin{2\varphi}} = \frac{R}{\sin\varphi}\]

\[AB = \frac{2R \cdot \sin\varphi \cdot \cos\varphi}{\sin\varphi}\]

\[AB = 2R \cdot \cos\varphi.\]

\[S_{2} = S_{AA_{1}B_{1}B} = AB \cdot H =\]

\[= 2R \cdot \cos\varphi \cdot H;\]

\[\frac{S_{1}}{S_{2}} = \frac{2RH}{2RH \cdot \cos\varphi} = \frac{1}{\cos\varphi}.\]

\[Ответ:\ \ \frac{1}{\cos\varphi}.\]