Решебник по геометрии 10 класс Атанасян ФГОС 538

\[\boxed{\mathbf{538.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[Цилиндр(O,r,h);\]

\[\textbf{а)}\ S_{бок} = S;\]

\[S_{осн} = Q;\]

\[\textbf{б)}\ ABCD - квадрат;\]

\[HH_{1} = h;\]

\[\textbf{в)}\ ABCD - квадрат;\]

\[S_{ц} = S.\]

\[Найти:\]

\[\text{V.}\]

\[Решение.\]

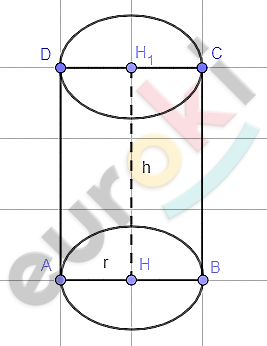
\[HH_{1} = h - высота\ цилиндра;\]

\[AH = BH = r - радиус\ \]

\[основания.\]

\[\textbf{а)}\ S_{бок} = S = 2\pi \bullet hr \rightarrow \ h =\]

\[= \frac{S}{2\pi r};\]

\[S_{осн} = Q = \pi r^{2} \rightarrow r^{2} = \frac{Q}{\pi};\]

\[h = \frac{S}{2\pi\sqrt{r^{2}}} = \frac{S}{2\pi\sqrt{\frac{Q}{\pi}}} = \frac{S}{2\sqrt{\text{πQ}}};\]

\[V = \pi r^{2}h = \pi \bullet \frac{Q}{\pi} \bullet \frac{S}{2\sqrt{\text{πQ}}} =\]

\[= \frac{S}{2}\sqrt{\frac{Q^{2}}{\text{πQ}}} = \frac{S}{2}\sqrt{\frac{Q}{\pi}}.\]

\[\textbf{б)}\ ABCD - квадрат:\ \]

\[d = h = 2r \rightarrow r = \frac{h}{2}.\]

\[V = \pi r^{2}h = \pi \bullet \frac{h^{2}}{4} \bullet h = \frac{\pi h^{3}}{4}.\]

\[\textbf{в)}\ ABCD - квадрат:\]

\[d = h = 2r;\]

\[S = 2\pi r^{2} + 2\pi rh =\]

\[= 2\pi r^{2} + 4\pi r^{2} = 6\pi r^{2};\]

\[r = \sqrt{\frac{S}{6\pi}}.\]

\[V = \pi r^{2}h = \pi \bullet \frac{S}{6\pi} \bullet 2\sqrt{\frac{s}{6\pi}} =\]

\[= \frac{S}{6} \bullet \sqrt{\frac{2S}{3\pi}}.\]

\[\mathbf{Отв}ет:\ \ а)\ \frac{S}{2}\sqrt{\frac{Q}{\pi}};\ \ \]

\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ б)\ \frac{\pi h^{3}}{4};\ \ \]

\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ в)\ \frac{S}{6}\sqrt{\frac{2S}{3\pi}}.\]