Решебник по геометрии 10 класс Атанасян ФГОС 524

\[\boxed{\mathbf{524.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[\text{ABC}A_{1}B_{1}C_{1} - прямоугольная\ \]

\[призма;\]

\[⊿ABC - прямоугольный;\]

\[V = 3\ м^{3};\]

\[S_{AA_{1}BB_{1}} = 3\ м^{2};\]

\[S_{CC_{1}BB_{1}} = 3\sqrt{5}.\]

\[Найти:\]

\[длины\ ребер.\]

\[Решение.\]

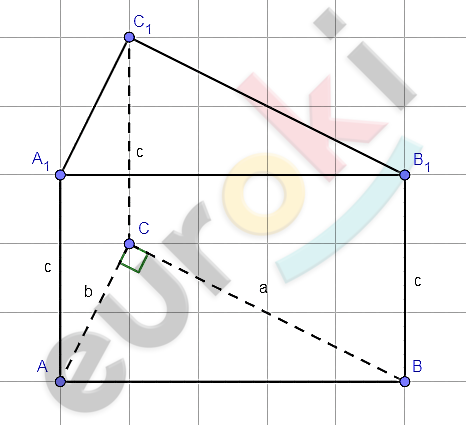
\[1)\ Пусть\ AC = b;\ \ BC = a;\ \ \]

\[AA_{1} = c;\ \ a < b:\ \]

\[AB = \sqrt{a^{2} + b^{2}}.\]

\[2)\ Площади\ боковых\ граней:\]

\[AA_{1}BB_{1} = c\sqrt{a^{2} + b^{2}};\ \ \ \]

\[AA_{1}CC_{1} = cb;\ \ \ \]

\[CC_{1}BB_{1} = ca.\]

\[3)\ S_{осн} = S_{\text{ABC}} = \frac{1}{2}ab:\ \]

\[V = \frac{1}{2}\text{abc.}\]

\[4)\ ac = 3;\ \ \ \ \frac{1}{2}abc = 3:\ \]

\[\frac{1}{2} \bullet 3 \bullet b = 3\ \ \]

\[b = 2\ м.\]

\[5)\ ac = 3\ м;\ \ \ \ c\sqrt{a^{2} + 4} =\]

\[= 3\sqrt{5}\ м:\]

\[a^{2}c^{2} = 9;\ \ \ c^{2}a^{2} + 4c^{2} = 45;\ \ \]

\[9 + 4c^{2} = 45.\]

\[Отсюда:\ \]

\[c = \sqrt{9} = 3\ м;\text{\ \ \ }\]

\[a = \frac{c}{3} = \frac{3}{3} = 1\ м.\ \ \]

\[7)\ \ AB = \ \sqrt{a^{2} + b^{2}} = \sqrt{1 + 4} =\]

\[= \sqrt{5}\ м.\]

\[Ответ:\ \ 1м;\ \ 2\ м;\ \ \sqrt{5}\ м;\ \ 3\ м.\]